Mercer theorem
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The bilinear series
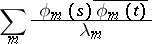 |
of a Hermitian positive-definite continuous kernel 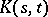 on
on 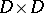 (cf. Integral equation with symmetric kernel; Kernel of an integral operator), where
(cf. Integral equation with symmetric kernel; Kernel of an integral operator), where 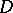 is the closure of a bounded domain in
is the closure of a bounded domain in 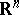 , converges absolutely and uniformly in
, converges absolutely and uniformly in 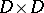 to
to 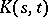 . Here the
. Here the 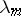 are the characteristic numbers of the kernel
are the characteristic numbers of the kernel 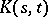 and the
and the 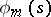 are the corresponding orthonormalized eigen functions. If a kernel
are the corresponding orthonormalized eigen functions. If a kernel 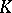 satisfies the conditions of Mercer's theorem, then the integral operator
satisfies the conditions of Mercer's theorem, then the integral operator 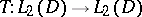 ,
,
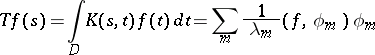 |
is nuclear (cf. Nuclear operator) and its trace 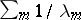 can be calculated by the formula
can be calculated by the formula
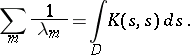 |
Mercer's theorem can be generalized to the case of a bounded discontinuous kernel.
The theorem was proved by J. Mercer [1].
References
| [1] | J. Mercer, Philos. Trans. Roy. Soc. London Ser. A , 209 (1909) pp. 415–446 |
| [2] | J. Mercer, "Functions of positive and negative type, and their connection with the theory of integral equations" Proc. Roy. Soc. London Ser. A , 83 (1908) pp. 69–70 |
| [3] | I.G. Petrovskii, "Lectures on the theory of integral equations" , Graylock (1957) (Translated from Russian) |
| [4] | F.G. Tricomi, "Integral equations" , Interscience (1957) |
| [5] | M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian) |
Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977) |
| [a2] | A.C. Zaanen, "Linear analysis" , North-Holland (1956) |
How to Cite This Entry:
Mercer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mercer_theorem&oldid=11889
Mercer theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mercer_theorem&oldid=11889
This article was adapted from an original article by V.B. Korotkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article