Difference between revisions of "MediaWiki:Sidebar"
| Line 82: | Line 82: | ||
====References==== | ====References==== | ||
| − | + | <html><table><TR><TD valign="top">[a1]</TD> | |
| + | <TD valign="top"> | ||
| + |  E. Sverdrup,  | ||
| + |  "Laws and chance variations" | ||
| + | , '''1''' | ||
| + | , North-Holland | ||
| + |  (1967) | ||
| + |  pp. 214ff</TD></TR></table></html> | ||
Revision as of 08:38, 17 June 2010
A conditional probability distribution of a random variable, to be contrasted with its unconditional or a priori distribution.
Let
<html> be a random parameter with an a priori density
be a random parameter with an a priori density
 ,
let
,
let
 be a random result of observations and let
be a random result of observations and let
 be the conditional density of
be the conditional density of
 when
when
 ;
then the a posteriori distribution of
;
then the a posteriori distribution of
 for a given
for a given
 </html>,
according to the
Bayes formula,
has the density
</html>,
according to the
Bayes formula,
has the density
<html>
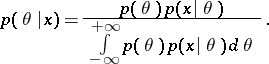 |
</html>
If
<html> </html>
is a
sufficient statistic
for the family of distributions with densities
<html>
</html>
is a
sufficient statistic
for the family of distributions with densities
<html> ,
then the a posteriori distribution depends not on
,
then the a posteriori distribution depends not on
 itself, but on
itself, but on
 .
The asymptotic behaviour of the a posteriori distribution
.
The asymptotic behaviour of the a posteriori distribution
 as
as
 ,
where
,
where
 are the results of independent observations with density
are the results of independent observations with density
 ,</html>
is
"almost independent"
of the a priori distribution of
<html>
,</html>
is
"almost independent"
of the a priori distribution of
<html> </html>.
</html>.
For the role played by a posteriori distributions
in the theory of statistical decisions, see
Bayesian approach.
References
<html>
| [1] |
S.N. Bernshtein, "Probability theory" , Moscow-Leningrad (1946) (In Russian) |
</html>
Yu.V. Prokhorov
Comments
References
<html>
| [a1] |
E. Sverdrup, "Laws and chance variations" , 1 , North-Holland (1967) pp. 214ff |
</html>
Sidebar. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sidebar&oldid=3003