Measure space
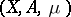
A measurable space  with a measure
with a measure 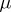 given on
given on 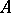 (i.e. a countably-additive function
(i.e. a countably-additive function 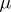 with values in
with values in  for which
for which 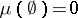 ; the latter property follows from additivity if the measure is finite, i.e. does not take the value
; the latter property follows from additivity if the measure is finite, i.e. does not take the value  , or even if there is some
, or even if there is some 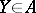 with
with 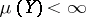 ). The notation
). The notation 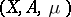 is often shortened to
is often shortened to 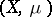 and one says that
and one says that 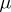 is a measure on
is a measure on  ; sometimes the notation is shortened to
; sometimes the notation is shortened to  . The basic case is when
. The basic case is when 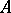 is a
is a  -algebra (cf. Algebra of sets) and
-algebra (cf. Algebra of sets) and 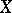 can be represented as
can be represented as  with
with  and
and 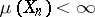 . In this case the measure is called (totally)
. In this case the measure is called (totally)  -finite (while if
-finite (while if  , then it is called (totally) finite). Such is, e.g., the Lebesgue measure on
, then it is called (totally) finite). Such is, e.g., the Lebesgue measure on  (cf. Lebesgue space). However, sometimes non-
(cf. Lebesgue space). However, sometimes non- -finite measures are encountered, such as, e.g., the
-finite measures are encountered, such as, e.g., the 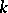 -dimensional Hausdorff measure on
-dimensional Hausdorff measure on 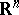 for
for  . One may also encounter modifications in which
. One may also encounter modifications in which 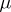 takes values in
takes values in 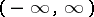 , or complex or vector values, as well as cases when
, or complex or vector values, as well as cases when 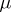 is only finitely additive.
is only finitely additive.
References
| [1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [2] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
Measure space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measure_space&oldid=14867