Mazur-Orlicz theorem
A sequence  is said to be summable to
is said to be summable to  by a method
by a method  given by an infinite matrix
given by an infinite matrix  , if
, if
 |
Let  be the set of all sequences summables by a method
be the set of all sequences summables by a method  . Such a method is said to be convergence preserving if
. Such a method is said to be convergence preserving if  contains all convergent sequences (it is not assumed, however, that for a convergent sequence
contains all convergent sequences (it is not assumed, however, that for a convergent sequence  one has
one has  ; if the latter holds,
; if the latter holds,  is called a permanent summability method). For a convergence-preserving method
is called a permanent summability method). For a convergence-preserving method 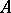 there is a well-defined quantity
there is a well-defined quantity
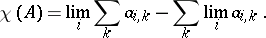 |
Let 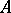 and
and  be convergence-preserving methods with
be convergence-preserving methods with  , and assume that for each convergent sequence
, and assume that for each convergent sequence  one has
one has  . Then the Mazur–Orlicz theorem is usually given to the following statement: If every bounded sequence in
. Then the Mazur–Orlicz theorem is usually given to the following statement: If every bounded sequence in  is in
is in 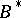 , then also for these sequences
, then also for these sequences  ([a3], Thm. 2; see also [a1] and [a2]).
([a3], Thm. 2; see also [a1] and [a2]).
A related result is as follows. If 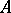 is a convergence-preserving method, then
is a convergence-preserving method, then 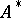 contains an unbounded sequence if either of the following is satisfied ([a3], Thm. 7):
contains an unbounded sequence if either of the following is satisfied ([a3], Thm. 7):
i) 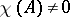 ;
;
ii)  and
and 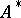 contains a bounded divergent sequence. A permanent method
contains a bounded divergent sequence. A permanent method  is said to be perfectly inconsistent if for each divergent sequence
is said to be perfectly inconsistent if for each divergent sequence  in
in  there is a permanent method
there is a permanent method 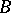 with
with  and
and  .
.
A permanent method  is perfectly inconsistent if and only if every sequence in
is perfectly inconsistent if and only if every sequence in  is either convergent or unbounded ([a3], Thm. 10).
is either convergent or unbounded ([a3], Thm. 10).
S. Mazur and W. Orlicz also worked also in functional analysis; e.g., the Banach–Steinhaus theorem for 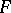 -spaces (see Fréchet topology) is due to them.
-spaces (see Fréchet topology) is due to them.
References
| [a1] | A.L. Brudno, "Summability of bounded sequences by means of matrices" Mat. Sb. , 16 (1949) pp. 191–247 (In Russian) |
| [a2] | S. Mazur, W. Orlicz, "Sur les mèthodes linèaires de sommation" C.R. Acad. Sci. Paris , 196 (1933) pp. 32–34 |
| [a3] | S. Mazur, W. Orlicz, "On linear methods of summability" Studia Math. , 14 (1954) pp. 129–160 |
Mazur-Orlicz theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mazur-Orlicz_theorem&oldid=12108