Maximum principle
discrete
The Pontryagin maximum principle for discrete-time control processes. For such a process the maximum principle need not be satisfied, even if the Pontryagin maximum principle is valid for its continuous analogue, obtained by replacing the finite difference operator 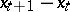 by the differential
by the differential  . For example, consider the optimal control problem
. For example, consider the optimal control problem
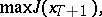 | (1) |
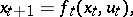 | (2) |
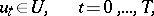 | (3) |
 | (4) |
This can be treated as a standard problem on an extremum in the presence of constraints. Then the condition for optimality of a trajectory 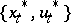 can be obtained with the help of the Lagrange function
can be obtained with the help of the Lagrange function
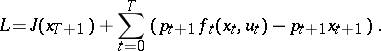 |
Here
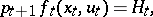 |
by analogy with the continuous case, is called the Hamilton function. Let 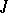 ,
, 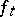 ,
,  , be differentiable functions with respect to all variables and let
, be differentiable functions with respect to all variables and let  be a bounded closed set. Then for a solution
be a bounded closed set. Then for a solution 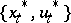 of (1)–(4) to be optimal it is necessary that there exist Lagrange multipliers
of (1)–(4) to be optimal it is necessary that there exist Lagrange multipliers 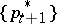 such that
such that 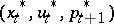 is a stationary point of the Lagrange function, that is, at this point
is a stationary point of the Lagrange function, that is, at this point
 |
for all admissible variations of the control 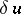 . The first condition leads to the dynamical equations of the discrete process (2) and the initial condition (4). The second leads to the boundary condition and the conjugate system for the impulses
. The first condition leads to the dynamical equations of the discrete process (2) and the initial condition (4). The second leads to the boundary condition and the conjugate system for the impulses 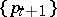 :
:
 |
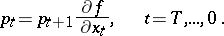 |
The third condition leads to a condition on the first variation of the Hamilton function:
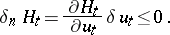 | (5) |
However, (5) does not imply that the Hamilton function attains its maximum at the optimal control,
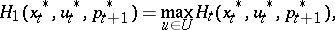 |
over all controls satisfying the constraint (3); it shows that 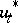 is a stationary point of the Hamilton function. If the first variation of the Hamilton function,
is a stationary point of the Hamilton function. If the first variation of the Hamilton function, 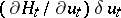 , is zero (this holds, in particular, when
, is zero (this holds, in particular, when 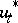 is an interior point or when there are admissible variations
is an interior point or when there are admissible variations 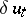 of the control at
of the control at 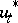 orthogonal to
orthogonal to 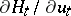 ), then the nature of the stationary point is determined by the successive terms in the expansion:
), then the nature of the stationary point is determined by the successive terms in the expansion:
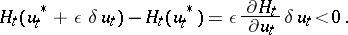 |
Examples have been constructed in which  is a local maximum, a local minimum and even a saddle point of the Hamilton function. Therefore, in general, the maximum principle does not hold for discrete systems.
is a local maximum, a local minimum and even a saddle point of the Hamilton function. Therefore, in general, the maximum principle does not hold for discrete systems.
For systems which are linear in the phase variables,
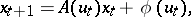 |
or in the controls,
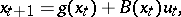 |
under the additional condition of linearity of the objective 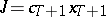 in the first case, or convexity of
in the first case, or convexity of 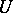 in the second case, the maximum principle is satisfied (see [1]–[5]).
in the second case, the maximum principle is satisfied (see [1]–[5]).
If the optimal control problem for a linear discrete system is treated as a linear programming problem (see [6], [7]), then its dual discrete-time dynamical problem may be obtained. The conjugate system for the impulses gives the dynamical equation for the dual problem. On an optimal trajectory not only the objective but also the Hamilton functions of dual dynamical systems coincide.
References
| [1] | L.-Ts. Fan, Ch.-S. Wang, "The discrete maximum principle" , Wiley (1964) |
| [2] | A.I. Propoi, "Elements of the theory of optimal processes" , Moscow (1973) (In Russian) |
| [3] | B.H. Pshenichnyi, "Necessary conditions for an extremum" , M. Dekker (1971) (Translated from Russian) |
| [4] | V.G. Boltyanskii, "Optimal control of discrete systems" , Wiley (1978) (Translated from Russian) |
| [5] | R. Gabasov, F.M. Kirillova, "Extending L.S. Pontryagin's maximum principle to discrete systems" Automation and Remote Control , 27 (1966) pp. 1878–1882 Avtomatika i Telemekhanika , 11 (1966) pp. 46–51 |
| [6] | Yu.P. Ivanilov, "Conjugate (dual) linear dynamic optimization problems and procedures for their computation" Prikl. Mat. i Programmirov. , 4 (1971) pp. 31–40 (In Russian) |
| [7] | Yu.P. Ivanilov, A.I. Propoi, "On linear dynamic programming problems" Soviet Math. Dokl. , 12 : 3 (1971) pp. 926–930 Dokl. Akad. Nauk SSSR , 198 : 5 (1971) pp. 1011–1014 |
Comments
For the maximum principle for analytic functions see Maximum-modulus principle.
References
| [a1] | A.E. Bryson, Y.-C. Ho, "Applied optimal control" , Ginn (1969) |
Maximum principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximum_principle&oldid=14552