Maximal spectral type

The type of the maximal spectral measure (i.e. its equivalence class) of a normal operator acting on a Hilbert space . This measure is defined (up to equivalence) by the following condition. Let be the resolution of the identity in the spectral representation of the normal operator , and let (where denotes a Borel set) be the associated "operator-valued" measure. Then precisely for those for which 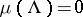. Any 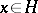has an associated spectral measure ; in these terms the definition of implies that for any the measure is absolutely continuous with respect to and there is an for which is equivalent to (that is, has maximal spectral type). If is separable, then a measure with these properties always exists, but if is not separable, then there is no such measure and does not have maximal spectral type. This complicates the theory of unitary invariants of normal operators in the non-separable case.

References

[1]	A.I. Plesner, "Spectral theory of linear operators" , F. Ungar (1969) (Translated from Russian)