Maximal ergodic theorem
If 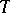 is an endomorphism of a measure space
is an endomorphism of a measure space 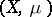 , if
, if 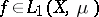 and if
and if 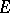 is the set of
is the set of 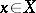 for which
for which
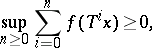 |
then
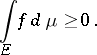 |
The maximal ergodic theorem is due to K. Yosida and S. Kakutani [1], who showed that it can play a central role in the proof of the Birkhoff ergodic theorem (G.D. Birkhoff himself, instead of the maximal ergodic theorem, used somewhat different arguments). In later proofs of generalizations of Birkhoff's theorem (and also in related questions on the decomposition of the phase space into conservative and dissipative parts under conditions such that these generalizations make sense) a generalized maximal ergodic theorem is used in a similar way. There is a generalization of the maximal ergodic theorem due to E. Hopf and a simple proof of this generalization was given by A. García (see [2]). See also [3] and the references in Birkhoff ergodic theorem.
References
| [1] | K. Yosida, S. Kakutani, "Birkhoff's ergodic theorem and the maximal ergodic theorem" Proc. Imp. Acad. Tokyo , 15 (1939) pp. 165–168 |
| [2] | J. Neveu, "Mathematical foundations of the calculus of probability" , Holden-Day (1965) (Translated from French) |
| [3] | A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with invariant measure" Progress in Math. , 8 (1970) pp. 151–215 Itogi Nauk. Anal. (1967) pp. 133–187 |
Comments
A variety of ergodic theorems (including historical remarks) can be found in [a1].
References
| [a1] | U. Krengel, "Ergodic theorems" , de Gruyter (1985) |
Maximal ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_ergodic_theorem&oldid=17718