Maximal correlation coefficient
From Encyclopedia of Mathematics
A measure of dependence of two random variables 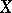 and
and 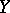 , defined as the least upper bound of the values of the correlation coefficients between the real random variables
, defined as the least upper bound of the values of the correlation coefficients between the real random variables 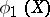 and
and 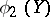 , which are functions of
, which are functions of 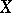 and
and 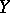 such that
such that 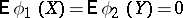 and
and 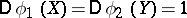 :
:
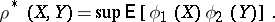 |
If this least upper bound is attained at 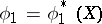 and
and 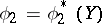 , then the maximal correlation coefficient between
, then the maximal correlation coefficient between 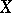 and
and 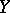 is equal to the correlation coefficient of
is equal to the correlation coefficient of 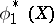 and
and 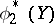 . The maximal correlation coefficient has the property:
. The maximal correlation coefficient has the property: 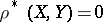 is necessary and sufficient for the independence of
is necessary and sufficient for the independence of 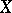 and
and 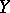 . If there is a linear correlation between the variables, then the maximal correlation coefficient coincides with the usual correlation coefficient.
. If there is a linear correlation between the variables, then the maximal correlation coefficient coincides with the usual correlation coefficient.
References
| [1] | O.V. Sarmanov, "The maximum correlation coefficient (symmetric case)" Dokl. Akad. Nauk SSSR , 120 : 4 (1958) pp. 715–718 (In Russian) |
| [2] | O.V. Sarmanov, Dokl. Akad. Nauk SSSR , 53 : 9 (1946) pp. 781–784 |
| [3] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
Comments
See also Canonical correlation.
References
| [a1] | H. Gebelein, "Das statistische Problem der Korrelation als Variations- und Eigenwertproblem und sein Zusammenhang mit der Ausgleichungrechnung" Z. Angew. Math. Mech. , 21 (1941) pp. 364–379 |
| [a2] | R. Koyak, "On measuring internal dependence in a set of random variables" Ann. Statist. , 15 (1987) pp. 1215–1229 |
How to Cite This Entry:
Maximal correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_correlation_coefficient&oldid=19195
Maximal correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_correlation_coefficient&oldid=19195
This article was adapted from an original article by I.O. Sarmanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article