Matrix tree theorem
Let  be a graph with
be a graph with  vertices
vertices 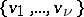 and
and  edges
edges  , some of which may be oriented. The incidence matrix of
, some of which may be oriented. The incidence matrix of  is the
is the 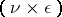 -matrix
-matrix  whose entries are given by
whose entries are given by  if
if 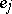 is a non-oriented link (i.e. an edge that is not a loop) incident to
is a non-oriented link (i.e. an edge that is not a loop) incident to 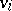 or if
or if 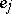 is an oriented link with head
is an oriented link with head  ,
, 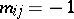 if
if 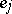 is an oriented link with tail
is an oriented link with tail 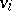 ,
,  if
if 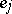 is a loop (necessarily non-oriented) at
is a loop (necessarily non-oriented) at 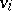 , and
, and 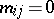 otherwise. The mixed Laplacian matrix of
otherwise. The mixed Laplacian matrix of 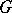 is defined as
is defined as 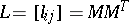 . It is easy to see that the diagonal entries of
. It is easy to see that the diagonal entries of 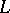 give the degrees of the vertices with, however, each loop contributing
give the degrees of the vertices with, however, each loop contributing 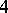 to the count, and the off-diagonal entry
to the count, and the off-diagonal entry 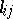 gives the number of non-oriented edges joining
gives the number of non-oriented edges joining  and
and  minus the number of oriented edges joining them. Let
minus the number of oriented edges joining them. Let  denote the number of spanning trees of
denote the number of spanning trees of 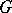 , with orientation ignored.
, with orientation ignored.
The matrix tree theorem in its classical form, which is already implicit in the work of G. Kirchhoff [a9], states that if  is the Laplacian of any orientation of a loopless undirected graph
is the Laplacian of any orientation of a loopless undirected graph 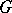 and
and  is the matrix obtained by deleting any row
is the matrix obtained by deleting any row  and column
and column 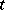 of
of 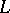 , then
, then 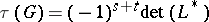 ; that is, each cofactor of
; that is, each cofactor of  is equal to the tree-number of
is equal to the tree-number of  . If
. If  denotes the adjoint of the matrix
denotes the adjoint of the matrix 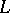 and
and 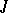 denotes the matrix with all entries equal to
denotes the matrix with all entries equal to 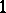 , then
, then 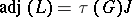 . The proof of this theorem uses the Binet–Cauchy theorem to expand the cofactor of
. The proof of this theorem uses the Binet–Cauchy theorem to expand the cofactor of 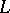 together with the fact that every non-singular
together with the fact that every non-singular 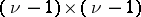 -minor of
-minor of 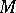 (cf. also Minor) comes from a spanning tree of
(cf. also Minor) comes from a spanning tree of 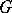 having value
having value 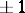 . In the case of the complete graph
. In the case of the complete graph 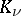 (with some orientation),
(with some orientation), 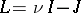 , and it can be seen that
, and it can be seen that  , which is Cayley's formula for the number of labelled trees on
, which is Cayley's formula for the number of labelled trees on  vertices [a4]. Temperley's result [a3], Prop. 6.4, avoids using the cofactor notation in the following form:
vertices [a4]. Temperley's result [a3], Prop. 6.4, avoids using the cofactor notation in the following form: 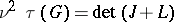 . It is interesting to note that this determinantal way of computing
. It is interesting to note that this determinantal way of computing 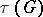 requires
requires 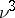 operations rather than the
operations rather than the 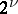 operations when using recursion [a17], p. 66.
operations when using recursion [a17], p. 66.
For a loopless directed graph 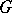 , let
, let 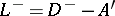 and
and 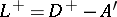 , where
, where 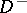 and
and 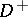 are the diagonal matrices of in-degrees and out-degrees in
are the diagonal matrices of in-degrees and out-degrees in 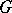 , and the
, and the 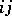 -entry of
-entry of 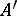 is the number of edges from
is the number of edges from 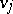 to
to 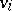 . An out-tree is an orientation of a tree having a root of in-degree
. An out-tree is an orientation of a tree having a root of in-degree  and all other vertices of in-degree
and all other vertices of in-degree 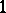 . An in-tree is an out-tree with its edges reversed. W.T. Tutte [a16] extended the matrix tree theorem by showing that the number of out-trees (respectively, in-trees) rooted at
. An in-tree is an out-tree with its edges reversed. W.T. Tutte [a16] extended the matrix tree theorem by showing that the number of out-trees (respectively, in-trees) rooted at 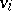 is the value of any cofactor in the
is the value of any cofactor in the  th row of
th row of 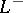 (respectively,
(respectively,  th column of
th column of  ). In fact, the principal minor of
). In fact, the principal minor of 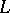 obtained by deleting rows and columns indexed by
obtained by deleting rows and columns indexed by 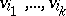 equals the number of spanning forests of
equals the number of spanning forests of 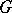 having precisely
having precisely 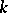 out-trees rooted at
out-trees rooted at 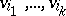 .
.
In all the approaches it is clear that the significant property of the Laplacian 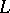 is that
is that 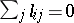 for
for 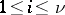 . By allowing
. By allowing 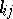 to be indeterminates over the field of rational numbers, the generating function version of the matrix tree theorem is obtained [a8], Sect. 3.3.25: The number of trees rooted at
to be indeterminates over the field of rational numbers, the generating function version of the matrix tree theorem is obtained [a8], Sect. 3.3.25: The number of trees rooted at  on the vertex set
on the vertex set 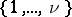 , with
, with 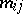 occurrences of the edge
occurrences of the edge 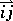 (directed away from the root), is the coefficient of the monomial
(directed away from the root), is the coefficient of the monomial 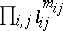 in the
in the 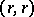 th cofactor of the matrix
th cofactor of the matrix 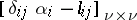 , where
, where 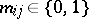 and
and 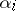 is the sum of the entries in the
is the sum of the entries in the 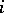 th row of
th row of  , for
, for 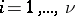 .
.
Several related identities can be found in work by J.W. Moon on labelled trees [a13]. For various proofs of Cayley's formula, see [a14].
Another direction of generalization is to interpret all the minors of the Laplacian rather than just the principal ones. Such generalizations can be found in [a5] and [a2], where arbitrary minors are expressed as signed sums over non-singular substructures that are more complicated than trees.
The edge version of the Laplacian is defined to be the 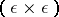 -matrix
-matrix 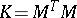 . The connection of its cofactors with the Wiener index in applications to chemistry is presented in [a11]. The combinatorial description of the arbitrary minors of
. The connection of its cofactors with the Wiener index in applications to chemistry is presented in [a11]. The combinatorial description of the arbitrary minors of 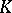 when
when 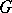 is a tree is studied in [a1].
is a tree is studied in [a1].
Applications are widespread. Variants of the matrix tree theorem are used in the topological analysis of passive electrical networks. The node-admittance matrix considered for this purpose is closely related to the Laplacian matrix (see [a10], Chap. 7). Abundance of forests suggests greater accessibility in networks. Due to this connection, the matrix tree theorem is used in developing distance concepts in social networks (see [a6]). The 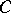 -matrix which occurs in the design of statistical experiments (cf. also Design of experiments) is the Laplacian of a graph associated with the design. In this context the matrix tree theorem is used to study
-matrix which occurs in the design of statistical experiments (cf. also Design of experiments) is the Laplacian of a graph associated with the design. In this context the matrix tree theorem is used to study 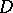 -optimal designs (see [a7], p. 67). Finally, the matrix tree theorem is closely related to the Perron–Frobenius theorem. If
-optimal designs (see [a7], p. 67). Finally, the matrix tree theorem is closely related to the Perron–Frobenius theorem. If 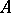 is the transition matrix of an irreducible Markov chain, then by the Perron–Frobenius theorem it admits a unique stationary distribution. This fact is easily deduced from the matrix tree theorem, which in fact gives an interpretation of the components of the stationary distribution in terms of tree-counts. This observation is used to approximate the stationary distribution of a countable Markov chain (see [a15], p. 222).
is the transition matrix of an irreducible Markov chain, then by the Perron–Frobenius theorem it admits a unique stationary distribution. This fact is easily deduced from the matrix tree theorem, which in fact gives an interpretation of the components of the stationary distribution in terms of tree-counts. This observation is used to approximate the stationary distribution of a countable Markov chain (see [a15], p. 222).
An excellent survey of interesting developments related to Laplacians may be found in [a12].
References
| [a1] | R.B. Bapat, J.W. Grossman, D.M. Kulkarni, "Edge version of the matrix tree theorem for trees" Linear and Multilinear Algebra , 47 (2000) pp. 217–229 |
| [a2] | R.B. Bapat, J.W. Grossman, D.M. Kulkarni, "Generalized matrix tree theorem for mixed graphs" Linear and Multilinear Algebra , 46 (1999) pp. 299–312 |
| [a3] | N. Biggs, "Algebraic graph theory" , Cambridge Univ. Press (1993) (Edition: Second) |
| [a4] | A. Cayley, "A theorem on trees" Quart. J. Math. , 23 (1889) pp. 376–378 |
| [a5] | S. Chaiken, "A combinatorial proof of the all minors matrix tree theorem" SIAM J. Algebraic Discr. Math. , 3 : 3 (1982) pp. 319–329 |
| [a6] | P.Yu. Chebotarev, E.V. Shamis, "The matrix-forest theorem and measuring relations in small social groups" Automat. Remote Control , 58 : 9:2 (1997) pp. 1505–1514 |
| [a7] | G.M. Constantine, "Combinatorial theory and statistical design" , Wiley (1987) |
| [a8] | I.P. Goulden, D.M. Jackson, "Combinatorial enumeration" , Wiley (1983) |
| [a9] | G. Kirchhoff, "Über die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Ströme geführt wird" Ann. Phys. Chem. , 72 (1847) pp. 497–508 |
| [a10] | W. Mayeda, "Graph theory" , Wiley (1972) |
| [a11] | R. Merris, "An edge version of the matrix-tree theorem and the Wiener index" Linear and Multilinear Algebra , 25 (1989) pp. 291–296 |
| [a12] | R. Merris, "Laplacian matrices of graphs: a survey" Linear Alg. & Its Appl. , 197/198 (1994) pp. 143–176 |
| [a13] | J.W. Moon, "Counting labeled trees" , Canad. Math. Monographs , 1 , Canad. Math. Congress (1970) |
| [a14] | J.W. Moon, "Various proofs of Cayley's formula for counting trees" F. Harary (ed.) , A Seminar on Graph Theory , Holt, Rinehart & Winston (1967) pp. 70–78 |
| [a15] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) (Edition: Second) |
| [a16] | W.T. Tutte, "The disection of equilateral triangles into equilateral triangles" Proc. Cambridge Philos. Soc. , 44 (1948) pp. 463–482 |
| [a17] | D.B. West, "Introduction to graph theory" , Prentice-Hall (1996) |
Matrix tree theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_tree_theorem&oldid=14639