Matrix summation method
One of the methods for summing series and sequences using an infinite matrix. Employing an infinite matrix 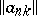 ,
, 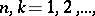 a given sequence
a given sequence 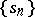 is transformed into the sequence
is transformed into the sequence 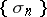 :
:
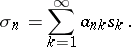 |
If the series on the right-hand side converges for all 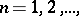 and if the sequence
and if the sequence 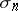 has a limit
has a limit  for
for 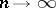 :
:
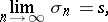 |
then the sequence  is said to be summable by the method determined by the matrix
is said to be summable by the method determined by the matrix 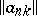 , or simply summable by the matrix
, or simply summable by the matrix 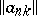 , and the number
, and the number  is referred to as its limit in the sense of this summation method. If
is referred to as its limit in the sense of this summation method. If 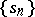 is regarded as the sequence of partial sums of a series
is regarded as the sequence of partial sums of a series
 | (1) |
then this series is said to be summable to the sum  by the matrix
by the matrix 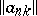 .
.
A matrix summation method for series can be also defined directly by transforming the series (1) into a sequence 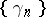 :
:
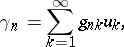 | (2) |
where 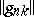 is a given matrix. In this case the series (1) is said to be summable to the sum
is a given matrix. In this case the series (1) is said to be summable to the sum  if, for all
if, for all 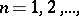 the series on the right-hand side in (2) converges and
the series on the right-hand side in (2) converges and
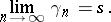 |
Less often used are matrix summation methods defined by a transformation of a series (1) into a series
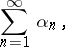 | (3) |
where
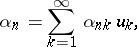 |
or by a transformation of a sequence 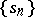 into a series
into a series
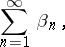 | (4) |
where
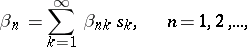 |
which use matrices 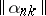 and
and 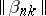 , respectively. In these cases the series (1) with the partial sums
, respectively. In these cases the series (1) with the partial sums 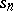 is summable to the sum
is summable to the sum  if the series (3) converges to
if the series (3) converges to  or, respectively, if the series (4) converges to
or, respectively, if the series (4) converges to  .
.
The matrix of a summation method all entries of which are non-negative is called a positive matrix. Among the matrix summation methods one finds, for example, the Voronoi summation method, the Cesàro summation methods, the Euler summation method, the Riesz summation method 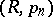 , the Hausdorff summation method, and others (see also Summation methods).
, the Hausdorff summation method, and others (see also Summation methods).
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.P. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 : 1 (1976) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Matrix summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_summation_method&oldid=12057