Matrix of transition probabilities
From Encyclopedia of Mathematics
The matrix  of transition probabilities in time
of transition probabilities in time  for a homogeneous Markov chain
for a homogeneous Markov chain  with at most a countable set of states
with at most a countable set of states  :
:
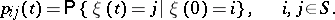 |
The matrices  of a Markov chain with discrete time or a regular Markov chain with continuous time satisfy the following conditions for any
of a Markov chain with discrete time or a regular Markov chain with continuous time satisfy the following conditions for any  and
and  :
:
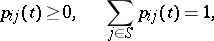 |
i.e. they are stochastic matrices (cf. Stochastic matrix), while for irregular chains
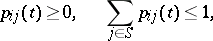 |
such matrices are called sub-stochastic.
By virtue of the basic (Chapman–Kolmogorov) property of a homogeneous Markov chain,
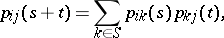 |
the family of matrices  forms a multiplicative semi-group; if the time is discrete, this semi-group is uniquely determined by
forms a multiplicative semi-group; if the time is discrete, this semi-group is uniquely determined by 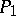 .
.
Comments
References
| [a1] | K.L. Chung, "Elementary probability theory with stochastic processes" , Springer (1974) |
How to Cite This Entry:
Matrix of transition probabilities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_of_transition_probabilities&oldid=13510
Matrix of transition probabilities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_of_transition_probabilities&oldid=13510
This article was adapted from an original article by A.M. Zubkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article