Massless Klein-Gordon equation
The Klein–Gordon equation [a1], [a2], [a3]
\begin{equation*} 0 = \left[ - \left( \frac { \partial } { \partial t } - i \frac { q e } { \hbar } \phi \right) ^ { 2 } + \right. \end{equation*}
\begin{equation*} \left.+ c ^ { 2 } \left( \nabla - i \frac { q e } { \hbar c } A \right) ^ { 2 } + \frac { c ^ { 4 } m ^ { 2 } } { \hbar ^ { 2 } } \right] \psi ( t , \mathbf{x} ) \end{equation*}
for the case where the mass parameter $m$ is equal to zero. The constant $c$ stands for the speed of light, $e$ is the charge of the positron, $\hbar = h / 2 \pi$ where $h$ is the Planck constant, $( t , \mathbf{x} )$ are the time, respectively space, variables, and $i$ is the imaginary unit. The (complex-valued) solution $\psi$ describes the wave function of a relativistic spinless and massless particle with charge 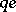 in the exterior electro-magnetic field $( \phi , \mathbf{A} )$. It is a second-order, hyperbolic partial differential equation. Solutions are being studied in, e.g., [a4], [a5].
in the exterior electro-magnetic field $( \phi , \mathbf{A} )$. It is a second-order, hyperbolic partial differential equation. Solutions are being studied in, e.g., [a4], [a5].
If the outer field is zero, $( \phi , \mathbf{A} ) = 0$, or the coupling of the spin to the magnetic potential $\mathbf{A}$ can be neglected, the massless Klein–Gordon equation also can be used for the description of massless spin-carrying particles, such as e.g. photons. In the case without outer fields the massless Klein–Gordon equation becomes equivalent to the wave equation with wave speed $c$ and is independent of the magnitude of Planck's constant $h$. This explains, why the wave nature of massless particles, such as e.g. photons ( "light" ), can also be observed on a macroscopic scale — in contrast with the wave nature of massive particles (cf.also Massless field; Massive field).
The interpretation of the wave function $\psi$ as a quantum mechanical "probability amplitude" (similarly as in the case of the Schrödinger equation), however, is not consistent, since the quantity $\int _ { \mathbf{R} ^ { 3 } } | \psi ( t , \mathbf{x} ) | ^ { 2 } d \mathbf{x}$ in general depends on the time parameter $t$. Furthermore, the existence of negative frequency solutions is in contrast with the required lower boundedness of the energy ( "stability of matter" ). These problems are resolved through a re-interpretation of $\psi ( t , \mathbf{x} )$ as a quantum field (cf. Quantum field theory), see e.g. [a6], [a7].
In recent time (as of 2000) solutions of the Klein–Gordon equation on Lorentzian manifolds have attracted increasing attention in connection with the theory of quantized fields on curved space-time, cf. e.g. [a8].
References
| [a1] | O. Klein, "Quantentheorie und fünfdimensionale Relativitätstheorie" Z. f. Phys. , 37 (1926) pp. 895 |
| [a2] | O. Gordon, "Der Comptoneffekt nach der Schrödingerschen Theorie" Z. f. Phys. , 40 (1926) pp. 117 |
| [a3] | E. Schrödinger, "Quantisierung als Eigenwertproblem IV" Ann. Phys. , 81 (1926) pp. 109 |
| [a4] | L. Gross, "Norm invariance of mass zero equations under the conformal group" J. Math. Phys. , 5 (1964) pp. 687–695 |
| [a5] | E.M. de Jager, "The Lorentz-invariant solutions of the Klein–Gordon equation I-II" Indag. Math. , 25 (1963) pp. 515–531; 546–558 |
| [a6] | R. Jost, "The general theory of quantised fields" , Amer. Math. Soc. (1965) |
| [a7] | S. Weinberg, "The quantum theory of fields" , I , Cambridge Univ. Press (1995) |
| [a8] | S.A. Fulling, "Aspects of quantum field theory in curved space-time" , Cambridge Univ. Press (1989) |
Massless Klein-Gordon equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Massless_Klein-Gordon_equation&oldid=50673