Massive field
A quantum field theory contains massive fields if the Hilbert space obtained by repeated application of these fields to the vacuum carries a unitary representation of the covering group of the orthochronous proper Poincaré group (cf. also Poincaré group) which fulfills the mass-gap condition: Let 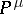 (
(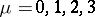 with
with  referring to the "time variable" ) be the generators of the space-time translations and let
referring to the "time variable" ) be the generators of the space-time translations and let 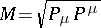 be the mass operator.
be the mass operator. 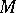 is well defined due to the positive-energy condition, i.e. the condition that the joint spectrum of
is well defined due to the positive-energy condition, i.e. the condition that the joint spectrum of 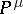 lies in the forward lightcone [a1]. The mass-gap condition then says that the spectrum of
lies in the forward lightcone [a1]. The mass-gap condition then says that the spectrum of 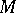 lies in
lies in 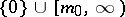 , where
, where 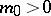 and the multiplicity of the zero-eigenvector of
and the multiplicity of the zero-eigenvector of 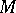 is one (uniqueness of the vacuum).
is one (uniqueness of the vacuum).
By the analysis of E. Wigner [a2], [a3], all states which describe a single particle form a Hilbert subspace carrying an irreducible representation of the Poincaré group which is labelled by a pair  . Here,
. Here, 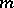 is the eigenvalue of these states with respect to the mass operator
is the eigenvalue of these states with respect to the mass operator 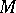 and
and 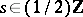 , called the "spin" of the particle, labels the finite-dimensional representation of the little group stabilizing a vector
, called the "spin" of the particle, labels the finite-dimensional representation of the little group stabilizing a vector  in the Minkowski space-time with
in the Minkowski space-time with 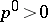 ,
, 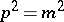 , i.e. the covering group of
, i.e. the covering group of 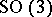 . As a consequence of the mass gap assumption, all particles in a theory with massive fields have positive mass
. As a consequence of the mass gap assumption, all particles in a theory with massive fields have positive mass 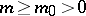 . Since one-particle states are usually assumed to be the states of lowest energy (above that of the vacuum), the mass-gap assumption and the assumption that a quantum field theory contains only particle states with positive mass, are considered as equivalent assumptions.
. Since one-particle states are usually assumed to be the states of lowest energy (above that of the vacuum), the mass-gap assumption and the assumption that a quantum field theory contains only particle states with positive mass, are considered as equivalent assumptions.
In the case that the one-particle states with the label 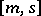 are separated from the rest of the mass spectrum by a second mass-gap, i.e. the spectrum of
are separated from the rest of the mass spectrum by a second mass-gap, i.e. the spectrum of 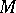 lies in
lies in 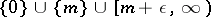 for some
for some 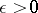 , and there is some quantum field
, and there is some quantum field 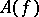 in the theory such that
in the theory such that 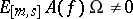 for some Schwartz test function
for some Schwartz test function 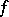 (cf. also Generalized functions, space of), with
(cf. also Generalized functions, space of), with 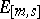 the projector on the Hilbert subspace on the
the projector on the Hilbert subspace on the 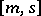 -one-particle states, one can apply the Haag–Ruelle scattering theory [a4], [a5], [a16] to
-one-particle states, one can apply the Haag–Ruelle scattering theory [a4], [a5], [a16] to 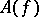 : Let
: Let 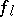 be Schwartz test functions, such that the Fourier transform
be Schwartz test functions, such that the Fourier transform 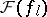 of
of  has support in the set
has support in the set 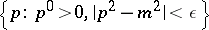 . Setting
. Setting 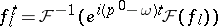 , one defines asymptotic fields by their action on the vacuum vector
, one defines asymptotic fields by their action on the vacuum vector  :
:
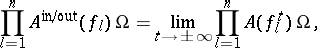 |
where the vectors on the right-hand side converge in the strong Hilbert space topology. The asymptotic fields 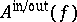 are free fields and generate a Fock space of multi-particle in- and out-states over the space of one-particle states with label
are free fields and generate a Fock space of multi-particle in- and out-states over the space of one-particle states with label 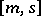 . If these in- and out-Fock spaces span the whole Hilbert space of the theory (the so-called requirement of asymptotic completeness) then, as a corollary to the PCT theorem, the scattering matrix taking in-states to the related out-states is unitary [a6]. The requirements of Haag–Ruelle theory alone suffice to derive the LSZ-reduction formulas [a7], which express the scattering matrix elements (scalar product of in- and out-states, which gives the physical transition amplitude) via the time-ordered vacuum expectation values of the field
. If these in- and out-Fock spaces span the whole Hilbert space of the theory (the so-called requirement of asymptotic completeness) then, as a corollary to the PCT theorem, the scattering matrix taking in-states to the related out-states is unitary [a6]. The requirements of Haag–Ruelle theory alone suffice to derive the LSZ-reduction formulas [a7], which express the scattering matrix elements (scalar product of in- and out-states, which gives the physical transition amplitude) via the time-ordered vacuum expectation values of the field 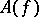 [a8]. This links the general formalism of quantum fields [a1], [a6] to the heuristic perturbation expansions for the time-ordered Wightman functions based on the classical Lagrangian and the heuristic path integral (cf. also Quantum field theory).
[a8]. This links the general formalism of quantum fields [a1], [a6] to the heuristic perturbation expansions for the time-ordered Wightman functions based on the classical Lagrangian and the heuristic path integral (cf. also Quantum field theory).
From the 1960s onwards, a systematic construction of rigorous (non-perturbative) models has been started in space-time dimensions 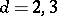 , see [a9], [a10], [a11]; for models with
, see [a9], [a10], [a11]; for models with 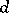 arbitrary (however with a state space carrying an indefinite inner product), see e.g. [a12].
arbitrary (however with a state space carrying an indefinite inner product), see e.g. [a12].
Massive quantum field theory is taken to be an approximation to the real physical situation, where all long range forces, associated with massless fields, can be neglected as "weak" in comparison with the strong short range forces associated with massive fields. If only massive fields are present in a theory, the mathematical treatment of the theory is simpler, due to the absence of a number of effects connected with massless particles and fields (cf. Massless field). However, several features of the contemporary (2000) physical theory of strong interactions, as e.g. "quarks" , "confinement" and "asymptotic freeness" , are not yet well explained in the given mathematical framework (but see e.g. [a13] for an interesting new approach).
Massive classical fields are studied in the framework of non-linear hyperbolic partial differential equations (cf. also Hyperbolic partial differential equation), see e.g. [a14], [a15].
References
| [a1] | R.F. Streater, A.S. Wightman, "PCT spin & statistics and all that " , Benjamin (1964) " , Benjamin (1964) |
| [a2] | E.P. Wigner, "On unitary representations of the inhomogenous Lorentz group" Ann. Math. , 40 (1939) pp. 149 |
| [a3] | W. Rühl, "The Lorentz group and harmonic analysis" , Benjamin (1970) |
| [a4] | R. Haag, "Quantum field theories with composite particles and asymptotic condition" Phys. Rev. , 112 (1958) pp. 669 |
| [a5] | D. Ruelle, "On the asymptotic condition in quantum field theory" Helv. Phys. Acta , 35 (1962) pp. 147 |
| [a6] | R. Jost, "The general theory of quantized fields" , Amer. Math. Soc. (1965) |
| [a7] | H. Lehmann, K. Symanzik, W. Zimmermann, "Zur Formulierung quantisierter Feldtheorien" Il Nuovo Cimento , 1 (1954) pp. 205 |
| [a8] | K. Hepp, "On the connection between LSZ and Wightman quantum field theory" Commun. Math. Phys. , 1 (1965) pp. 95 |
| [a9] | B. Simon, "The 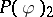 Euclidean (quantum) field theory" , Princeton Univ. Press (1975) Euclidean (quantum) field theory" , Princeton Univ. Press (1975) |
| [a10] | J. Glimm, A. Jaffe, "Quantum physics: A functional integral point of view" , Springer (1987) (Edition: Second) |
| [a11] | S. Albeverio, "Mathematical physics and stochastic analysis" Bell. Sci. Math. , 117 (1993) pp. 125 |
| [a12] | S. Albeverio, H. Gottschalk, J.-L. Wu, "Scattering behaviour of quantum vector fields obtained from Euclidean covariant SPDEs" Rept. Math. Phys. , 44 : 1 (1999) pp. 21 |
| [a13] | D. Buchholz, R. Vrech, "Scaling algebras and renormalization group in algebraic quantum field theory" Rev. Math. Phys. , 7 (1995) |
| [a14] | W. Strauss, "Nonlinear wave equations" , Amer. Math. Soc. (1989) |
| [a15] | S.B. Kuksin, "On the long-time behaviour of solutions of nonlinear wave equations" D. Iagolnitzer (ed.) , XIth Int. Cong. Math. Phys. , Cambridge Internat. Press (1995) pp. 273–277 |
| [a16] | R. Streater, "Uniqueness of the Haag–Ruelle scattering states" J. Math. Phys. , 8 (1967) pp. 1685–1693 |
Massive field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Massive_field&oldid=17599