Mass operator

operator of mass

The operator taking account of the interaction of a particle with its own field and other fields. Let the state of a system be described by the quantity

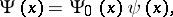where 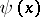is the field operator acting on the wave function 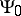(the state vector) and is a four-dimensional coordinate vector. If satisfies the equation

(*)

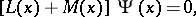where the operator 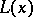corresponds to a free particle and 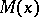accounts for its interaction with the particle's own field and other fields, then is called the mass operator. The mass operator is an integral operator with kernel :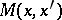

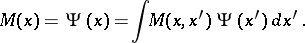The mass operator is closely related to the one-particle Green function 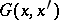, which is a solution of an equation similar to (*) but with a 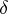-function source on the right-hand side:

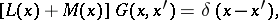where is the four-dimensional delta-function.

References

[1]	N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian)
[2]	A.A. Abrikosov, L.P. Gor'kov, I.E. Dzyaloshinskii, "Methods of quantum field theory in statistical physics" , Prentice-Hall (1963) (Translated from Russian)

Comments

The concept of a "mass operator" can only be given some sense in the context of quantum field perturbation theory, and plays a minor role in that context.