Markov function system
From Encyclopedia of Mathematics
A system 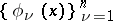 (
(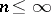 ) of linearly independent real-valued continuous functions defined on a finite interval
) of linearly independent real-valued continuous functions defined on a finite interval 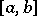 and satisfying the condition: For any finite
and satisfying the condition: For any finite 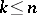 the functions
the functions 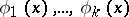 form a Chebyshev system on
form a Chebyshev system on 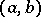 .
.
Examples of Markov function systems are:
a) 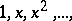 on any interval
on any interval 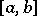 ;
;
b) 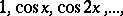 on
on 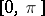 ;
;
c) 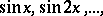 on
on  .
.
References
| [1] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
Comments
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) |
| [a2] | W.J. Studden, "Tchebycheff systems: with applications in analysis and statistics" , Wiley (1966) |
| [a3] | H.S. Shapiro, "Topics in approximation theory" , Springer (1971) |
| [a4] | I.M. Singer, "Best approximation in normed linear spaces by elements of linear subspaces" , Springer (1970) |
How to Cite This Entry:
Markov function system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_function_system&oldid=12310
Markov function system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_function_system&oldid=12310
This article was adapted from an original article by N.P. KorneichukV.P. Motornyi (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article