Markov chain, class of positive states of a
A set 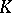 of states of a homogeneous Markov chain
of states of a homogeneous Markov chain 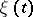 with state space
with state space 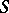 such that the transition probabilities
such that the transition probabilities
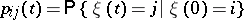 |
of 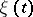 satisfy
satisfy
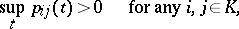 |
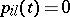 for any
for any 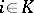 ,
,  ,
, 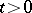 , and
, and
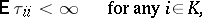 |
where 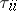 is the return time to the state
is the return time to the state 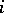 :
:
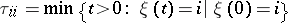 |
for a discrete-time Markov chain, and
 |
for a continuous-time Markov chain. When 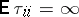 ,
, 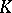 is called a zero class of states (class of zero states).
is called a zero class of states (class of zero states).
States in the same positive class 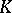 have a number of common properties. For example, in the case of discrete time, for any
have a number of common properties. For example, in the case of discrete time, for any 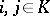 the limit relation
the limit relation
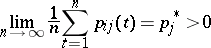 |
holds; if
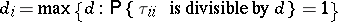 |
is the period of state 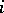 , then
, then 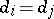 for any
for any 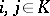 and
and 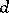 is called the period of the class
is called the period of the class 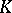 ; for any
; for any 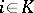 the limit relation
the limit relation
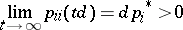 |
holds. A discrete-time Markov chain such that all its states form a single positive class of period 1 serves as an example of an ergodic Markov chain (cf. Markov chain, ergodic).
References
| [1] | K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1967) |
| [2] | J.L. Doob, "Stochastic processes" , Wiley (1953) |
Comments
Cf. also Markov chain, class of zero states of a for additional refences.
Markov chain, class of positive states of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_class_of_positive_states_of_a&oldid=14075