Difference between revisions of "Markov braid theorem"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 9 formulas, 7 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
If two closed braids represent the same ambient isotopy class of oriented links (cf. also [[Braid theory|Braid theory]]), then one can transform one braid to another by a sequence of Markov moves: | If two closed braids represent the same ambient isotopy class of oriented links (cf. also [[Braid theory|Braid theory]]), then one can transform one braid to another by a sequence of Markov moves: | ||
| − | i) | + | i) $a \leftrightarrow b a b ^ { - 1 }$ (conjugation). |
| − | ii) | + | ii) $a \leftrightarrow a b ^ { \pm 1 }_ { n }$, where $a$ is an element of the $n$th [[braid group]] |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130050/m1300505.png"/></td> </tr></table> |
| − | and | + | and $b _ { n }$ is the $n$th generator of the $( n + 1 )$th braid group. |
Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the [[Jones–Conway polynomial|Jones–Conway polynomial]]). | Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the [[Jones–Conway polynomial|Jones–Conway polynomial]]). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> J.S. Birman, "Braids, links and mapping class groups", ''Ann. of Math. Stud.'', '''82''' , Princeton Univ. Press (1974)</td></tr> | ||
| + | <tr><td valign="top">[a2]</td> <td valign="top"> A.A. Markov, "Über die freie Äquivalenz der geschlossenen Zöpfe", ''Recueil Math. Moscou'', '''1''' (1935) pp. 73–78 {{ZBL|0014.04202}}</td></tr> | ||
| + | <tr><td valign="top">[a3]</td> <td valign="top"> N.M. Weinberg, "On free equivalence of free braids", ''C.R. (Dokl.) Acad. Sci. USSR'', '''23''' (1939) pp. 215–216 (In Russian)</td></tr> | ||
| + | </table> | ||
Latest revision as of 08:04, 19 March 2023
If two closed braids represent the same ambient isotopy class of oriented links (cf. also Braid theory), then one can transform one braid to another by a sequence of Markov moves:
i) $a \leftrightarrow b a b ^ { - 1 }$ (conjugation).
ii) $a \leftrightarrow a b ^ { \pm 1 }_ { n }$, where $a$ is an element of the $n$th braid group
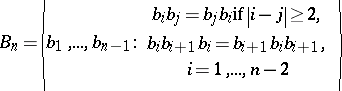 |
and $b _ { n }$ is the $n$th generator of the $( n + 1 )$th braid group.
Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the Jones–Conway polynomial).
References
| [a1] | J.S. Birman, "Braids, links and mapping class groups", Ann. of Math. Stud., 82 , Princeton Univ. Press (1974) |
| [a2] | A.A. Markov, "Über die freie Äquivalenz der geschlossenen Zöpfe", Recueil Math. Moscou, 1 (1935) pp. 73–78 Zbl 0014.04202 |
| [a3] | N.M. Weinberg, "On free equivalence of free braids", C.R. (Dokl.) Acad. Sci. USSR, 23 (1939) pp. 215–216 (In Russian) |
How to Cite This Entry:
Markov braid theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_braid_theorem&oldid=17995
Markov braid theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_braid_theorem&oldid=17995
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article