Mangoldt function
From Encyclopedia of Mathematics
The arithmetic function defined by
 |
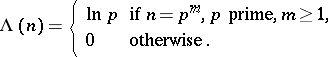The function 
has the following properties:
 |
 |
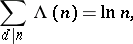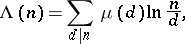where the sums are taken over all divisors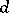 
of 
. The Mangoldt function is closely connected with the Riemann zeta-function 
. In fact, the generating series for 
is the logarithmic derivative of 
:
 |
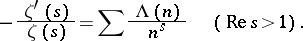The Mangoldt function was proposed by H. Mangoldt in 1894.
Comments
In the article above,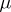 
denotes the Möbius function.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Sect. 17.7 |
How to Cite This Entry:
Mangoldt function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mangoldt_function&oldid=14110
Mangoldt function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mangoldt_function&oldid=14110
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article