Mahler problem

A conjecture in the metric theory of Diophantine approximation (cf. Diophantine approximation, metric theory of) stated by K. Mahler [1]: For almost-all (in the sense of the Lebesgue measure) numbers 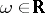the inequality

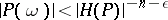has a finite number of solutions in polynomials 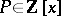of degree not exceeding . Here , is a natural number and 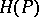is the maximum modulus of the coefficients of 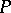. An equivalent formulation is: For almost-all 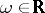the inequality

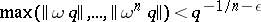has a finite number of solutions in integers 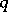( 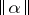is the distance from to the nearest integer).

Mahler's problem was solved affirmatively in 1964 by V.G. Sprindzhuk [2]. He also proved similar results for complex and 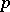-adic numbers, and also for power series over finite fields.

References

[1]	K. Mahler, "Ueber das Mass der Menge aller 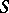-Zahlen" Math. Ann. , 106 (1932) pp. 131–139
[2]	V.G. Sprindzhuk, "Mahler's problem in metric number theory" , Amer. Math. Soc. (1969) (Translated from Russian)

Comments

The original paper of Sprindzhuk is [a1].

References

[a1]	V.G. Sprindzhuk, "A proof of Mahler's conjecture on the measure of the set of 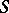numbers" Izv. Akad. Nauk SSSR Ser. Mat. , 29 (1965) pp. 379–436