Magnetic monopole
In physics, the phrase "magnetic monopole" usually denotes a Yang–Mills potential  and Higgs field
and Higgs field  whose equations of motion are determined by the Yang–Mills–Higgs action
whose equations of motion are determined by the Yang–Mills–Higgs action
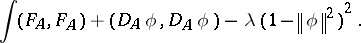 |
In mathematics, the phrase customarily refers to a static solution to these equations in the Bogomolny–Prasad–Sommerfield limit  which realizes, within its topological class, the absolute minimum of the functional
which realizes, within its topological class, the absolute minimum of the functional
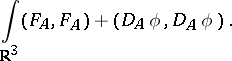 |
This means that it is a connection  on a principal
on a principal  -bundle over
-bundle over  (cf. also Connections on a manifold; Principal
(cf. also Connections on a manifold; Principal  -object) and a section
-object) and a section 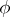 of the associated adjoint bundle of Lie algebras such that the curvature
of the associated adjoint bundle of Lie algebras such that the curvature 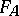 and covariant derivative
and covariant derivative 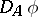 satisfy the Bogomolny equations
satisfy the Bogomolny equations
 |
and the boundary conditions
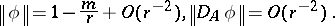 |
Pure mathematical advances in the theory of monopoles from the 1980s onwards have often proceeded on the basis of physically motivated questions.
The equations themselves are invariant under gauge transformations and orientation-preserving isometries. When  is large,
is large, 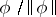 defines a mapping from a
defines a mapping from a  -sphere of radius
-sphere of radius  in
in 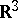 to an adjoint orbit
to an adjoint orbit 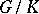 and the homotopy class of this mapping is called the magnetic charge. Most work has been done in the case
and the homotopy class of this mapping is called the magnetic charge. Most work has been done in the case 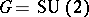 , where the charge is a positive integer
, where the charge is a positive integer 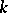 . The absolute minimum value of the functional is then
. The absolute minimum value of the functional is then 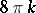 and the coefficient
and the coefficient 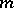 in the asymptotic expansion of
in the asymptotic expansion of 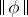 is
is 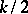 .
.
The first 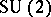 solution was found by E.B. Bogomolny, M.K. Prasad and C.M. Sommerfield in 1975. It is spherically symmetric of charge
solution was found by E.B. Bogomolny, M.K. Prasad and C.M. Sommerfield in 1975. It is spherically symmetric of charge 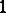 and has the form
and has the form
 |
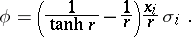 |
In 1980, C.H. Taubes [a10] showed by a gluing construction that there exist solutions for all larger 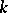 and soon after explicit axially-symmetric solutions were found. The first exact solution in the general case was given in 1981 by R.S. Ward for
and soon after explicit axially-symmetric solutions were found. The first exact solution in the general case was given in 1981 by R.S. Ward for 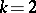 in terms of elliptic functions.
in terms of elliptic functions.
There are two ways of solving the Bogomolny equations. The first is by twistor methods. In the formulation of N.J. Hitchin [a6], an arbitrary solution corresponds to a holomorphic vector bundle over the complex surface 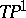 , the tangent bundle of the projective line. This is naturally isomorphic to the space of oriented straight lines in
, the tangent bundle of the projective line. This is naturally isomorphic to the space of oriented straight lines in 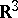 . The boundary conditions show that the holomorphic bundle is an extension of line bundles determined by a compact algebraic curve of genus
. The boundary conditions show that the holomorphic bundle is an extension of line bundles determined by a compact algebraic curve of genus 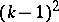 (the spectral curve) in
(the spectral curve) in 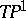 , satisfying certain constraints. The second method, due to W. Nahm [a12], involves solving an eigenvalue problem for the coupled Dirac operator and transforming the equations with their boundary conditions into a system of ordinary differential equations, the Nahm equations,
, satisfying certain constraints. The second method, due to W. Nahm [a12], involves solving an eigenvalue problem for the coupled Dirac operator and transforming the equations with their boundary conditions into a system of ordinary differential equations, the Nahm equations,
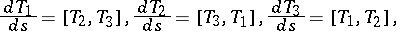 |
where 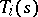 is a
is a 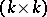 -matrix-valued function on
-matrix-valued function on  . Both constructions are based on analogous procedures for instantons, the key observation due to N.S. Manton being that the Bogomolny equations are dimensional reductions of the self-dual Yang–Mills equations (cf. also Yang–Mills field) in
. Both constructions are based on analogous procedures for instantons, the key observation due to N.S. Manton being that the Bogomolny equations are dimensional reductions of the self-dual Yang–Mills equations (cf. also Yang–Mills field) in 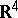 . The equivalence of the two methods for
. The equivalence of the two methods for 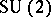 and their general applicability was established in [a7] (see also [a8]). Explicit formulas for
and their general applicability was established in [a7] (see also [a8]). Explicit formulas for 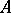 and
and  are difficult to obtain by either method, despite some exact solutions of Nahm's equations in symmetric situations [a5].
are difficult to obtain by either method, despite some exact solutions of Nahm's equations in symmetric situations [a5].
The case of a more general Lie group 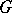 , where the stabilizer of
, where the stabilizer of 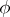 at infinity is a maximal torus, was treated by M.K. Murray [a11] from the twistor point of view, where the single spectral curve of an
at infinity is a maximal torus, was treated by M.K. Murray [a11] from the twistor point of view, where the single spectral curve of an 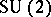 -monopole is replaced by a collection of curves indexed by the vertices of the Dynkin diagram of
-monopole is replaced by a collection of curves indexed by the vertices of the Dynkin diagram of 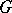 . The corresponding Nahm construction was described by J. Hurtubise and Murray [a9].
. The corresponding Nahm construction was described by J. Hurtubise and Murray [a9].
The moduli space (cf. also Moduli theory) of all 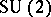 monopoles of charge
monopoles of charge 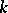 up to gauge equivalence was shown by Taubes [a14] to be a smooth non-compact manifold of dimension
up to gauge equivalence was shown by Taubes [a14] to be a smooth non-compact manifold of dimension 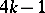 . Restricting to gauge transformations that preserve the connection at infinity gives a
. Restricting to gauge transformations that preserve the connection at infinity gives a 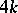 -dimensional manifold
-dimensional manifold 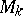 , which is a circle bundle over the true moduli space and carries a natural complete hyper-Kähler metric [a1] (cf. also Kähler–Einstein manifold). With respect to any of the complex structures of the hyper-Kähler family, this manifold is holomorphically equivalent to the space of based rational mappings of degree
, which is a circle bundle over the true moduli space and carries a natural complete hyper-Kähler metric [a1] (cf. also Kähler–Einstein manifold). With respect to any of the complex structures of the hyper-Kähler family, this manifold is holomorphically equivalent to the space of based rational mappings of degree 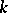 from
from  to itself [a3]. The metric is known in twistor terms [a1], and its Kähler potential can be written using the Riemann theta-function of the spectral curve [a8], but only the case
to itself [a3]. The metric is known in twistor terms [a1], and its Kähler potential can be written using the Riemann theta-function of the spectral curve [a8], but only the case 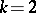 is known in a more conventional and usable form [a1] (as of 2000). This Atiyah–Hitchin manifold, the Euclidean Taub–NUT metric and
is known in a more conventional and usable form [a1] (as of 2000). This Atiyah–Hitchin manifold, the Euclidean Taub–NUT metric and 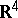 are the only
are the only 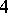 -dimensional complete hyper-Kähler manifolds with a non-triholomorphic
-dimensional complete hyper-Kähler manifolds with a non-triholomorphic 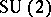 action. Its geodesics have been studied and a programme of Manton concerning monopole dynamics put into effect. Further dynamical features have been elucidated by P.M. Sutcliffe and C.J. Houghton [a15] using a mixture of numerical and analytical techniques.
action. Its geodesics have been studied and a programme of Manton concerning monopole dynamics put into effect. Further dynamical features have been elucidated by P.M. Sutcliffe and C.J. Houghton [a15] using a mixture of numerical and analytical techniques.
A cyclic 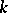 -fold covering of
-fold covering of 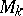 splits isometrically as a product
splits isometrically as a product 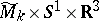 , where
, where 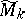 is the space of strongly centred monopoles. This space features in an application of
is the space of strongly centred monopoles. This space features in an application of 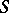 -duality in theoretical physics, and in [a13] G.B. Segal and A. Selby studied its topology and the
-duality in theoretical physics, and in [a13] G.B. Segal and A. Selby studied its topology and the  harmonic forms defined on it, partially confirming the physical predictions.
harmonic forms defined on it, partially confirming the physical predictions.
Magnetic monopoles on hyperbolic three-space were investigated from the twistor point of view by M.F. Atiyah [a2] (replacing the complex surface 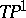 by the complement of the anti-diagonal in
by the complement of the anti-diagonal in 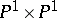 ) and in terms of discrete Nahm equations by Murray and M.A. Singer, [a16].
) and in terms of discrete Nahm equations by Murray and M.A. Singer, [a16].
References
| [a1] | M.F. Atiyah, N.J. Hitchin, "The geometry and dynamics of magnetic monopoles" , Princeton Univ. Press (1988) |
| [a2] | M.F. Atiyah, "Magnetic monopoles in hyperbolic space" , Vector bundles on algebraic varieties , Oxford Univ. Press (1987) pp. 1–34 |
| [a3] | S.K. Donaldson, "Nahm's equations and the classification of monopoles" Commun. Math. Phys. , 96 (1984) pp. 397–407 |
| [a4] | N.J. Hitchin, M.K. Murray, "Spectral curves and the ADHM method" Commun. Math. Phys. , 114 (1988) pp. 463–474 |
| [a5] | N.J. Hitchin, N.S. Manton, M.K. Murray, "Symmetric monopoles" Nonlinearity , 8 (1995) pp. 661–692 |
| [a6] | N.J. Hitchin, "Monopoles and geodesics" Commun. Math. Phys. , 83 (1982) pp. 579–602 |
| [a7] | N.J. Hitchin, "On the construction of monopoles" Commun. Math. Phys. , 89 (1983) pp. 145–190 |
| [a8] | N.J. Hitchin, "Integrable systems in Riemannian geometry" C.-L. Terng (ed.) K. Uhlenbeck (ed.) , Surveys in Differential Geometry , 4 , Internat. Press, Cambridge, Mass. (1999) pp. 21–80 |
| [a9] | J. Hurtubise, M.K. Murray, "On the construction of monopoles for the classical groups" Commun. Math. Phys. , 122 (1989) pp. 35–89 |
| [a10] | A. Jaffe, C.H. Taubes, "Vortices and monopoles" , Progress in Physics , 2 , Birkhäuser (1980) |
| [a11] | M.K. Murray, "Monopoles and spectral curves for arbitrary Lie groups" Commun. Math. Phys. , 90 (1983) pp. 263–271 |
| [a12] | W. Nahm, "The construction of all self-dual monopoles by the ADHM method" N.S. Craigie (ed.) P. Goddard (ed.) W. Nahm (ed.) , Monopoles in Quantum Field Theory , World Sci. (1982) |
| [a13] | G.B. Segal, A. Selby, "The cohomology of the space of magnetic monopoles" Commun. Math. Phys. , 177 (1996) pp. 775–787 |
| [a14] | C.H. Taubes, "Stability in Yang–Mills theories" Commun. Math. Phys. , 91 (1983) pp. 235–263 |
| [a15] | P.M. Sutcliffe, "BPS monopoles" Internat. J. Modern Phys. A , 12 (1997) pp. 4663–4705 |
| [a16] | M.K. Murray, "On the complete integrability of the discrete Nahm equations" Commun. Math. Phys. , 210 (2000) pp. 497–519 |
Magnetic monopole. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Magnetic_monopole&oldid=17620