Magic square
A square  array
array  composed of the integers from 1 up to
composed of the integers from 1 up to  and satisfying the following conditions:
and satisfying the following conditions:
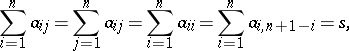 | (*) |
where  . There are also more general magic squares, in which
. There are also more general magic squares, in which  is not required.
is not required.
Any number  ,
,  , is uniquely characterized by a pair of residues
, is uniquely characterized by a pair of residues 
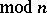 (the digits to base
(the digits to base  of
of 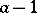 ), that is, by the points of the two-dimensional space
), that is, by the points of the two-dimensional space 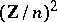 over the ring
over the ring 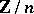 of residues modulo
of residues modulo  . Since the coordinates
. Since the coordinates 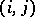 of the cells of the square may also be regarded as the elements of
of the cells of the square may also be regarded as the elements of 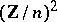 , it follows that any distribution of the numbers from 1 up to
, it follows that any distribution of the numbers from 1 up to 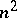 in an array
in an array 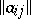 is given by a mapping
is given by a mapping
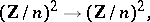 |
that is, by a pair of functions 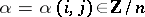 ,
, 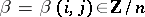 , where
, where  . The problem is to investigate those pairs that give magic squares. In general this has been done (see [1]) only under the additional assumption of linearity of
. The problem is to investigate those pairs that give magic squares. In general this has been done (see [1]) only under the additional assumption of linearity of 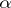 and
and 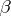 . It turns out, in particular, that magic squares with linear
. It turns out, in particular, that magic squares with linear  and
and  exist for odd
exist for odd  only.
only.
Already in the Middle Ages a number of algorithms for constructing magic squares of odd order  had been found. Each such algorithm is characterized by six residues
had been found. Each such algorithm is characterized by six residues  ,
,  ,
,  ,
, 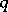 ,
,  ,
, 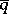 , and is described by the following rules: 1) the number 1 is put into the cell
, and is described by the following rules: 1) the number 1 is put into the cell  ; and 2) if
; and 2) if  was put into
was put into 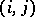 , then
, then 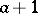 is put into
is put into  if that cell is still empty or into
if that cell is still empty or into  if
if 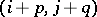 is occupied.
is occupied.
The residues 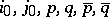 are not arbitrary but must satisfy certain conditions to ensure not only that (*) holds, but also that the algorithm is feasible, that is, that
are not arbitrary but must satisfy certain conditions to ensure not only that (*) holds, but also that the algorithm is feasible, that is, that  is empty when
is empty when 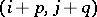 is occupied. These conditions are easily found (see [1]). Moreover, it turns out that a magic square can be constructed by an algorithm of this type if and only if the functions
is occupied. These conditions are easily found (see [1]). Moreover, it turns out that a magic square can be constructed by an algorithm of this type if and only if the functions 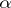 and
and 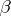 describing the square are linear.
describing the square are linear.
Many algorithms for constructing magic squares are known (resulting in squares with non-linear 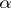 and
and 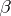 ), but there is no general theory for them (1989). Even the number of magic squares of order
), but there is no general theory for them (1989). Even the number of magic squares of order  is unknown (for
is unknown (for 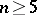 ; for
; for 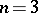 there is, up to obvious symmetries, only one magic square, whereas for
there is, up to obvious symmetries, only one magic square, whereas for 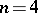 there are 880 magic squares).
there are 880 magic squares).
Magic squares having additional symmetry have also been investigated, again only in very special circumstances (for example, for 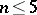 ; see [2]).
; see [2]).
References
| [1] | M.M. Postnikov, "Magic squares" , Moscow (1964) (In Russian) |
| [2] | E.Ya. Gurevich, "The secret of the Ancient Talisman" , Moscow (1969) (In Russian) |
Comments
Magic squares have been considered since ancient times. For instance, the magic square of order 3 was known in China around 2000 B.C.. Dürer's famous "Melancholy" shows a magic square of order 4.
There is a close connection between (pairs of orthogonal) Latin squares (cf. Latin square; Orthogonal Latin squares) and magic squares, which has been studied since L. Euler (see [a1] and [a2]). See also [a3] and the references given there.
References
| [a1] | L. Euler, "De quadratis magicis" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 7 , Teubner (1923) pp. 441–457 |
| [a2] | L. Euler, "Recherches sur une nouvelle espèce de quarrés magiques" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 7 , Teubner (1923) pp. 291–392 |
| [a3] | J. Dénes, A.D. Keedwell, "Latin squares and their applications" , English Univ. Press (1974) |
Magic square. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Magic_square&oldid=13333