Mackey topology
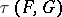 on a space
on a space  , being in duality with a space
, being in duality with a space  (over the same field)
(over the same field)
The topology of uniform convergence on the convex balanced subsets of 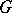 that are compact in the weak topology
that are compact in the weak topology 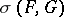 (defined by the duality between
(defined by the duality between  and
and 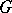 ). It was introduced by G.W. Mackey [1]. The Mackey topology is the strongest of the separated locally convex topologies (cf. Locally convex topology) which are compatible with the duality between
). It was introduced by G.W. Mackey [1]. The Mackey topology is the strongest of the separated locally convex topologies (cf. Locally convex topology) which are compatible with the duality between 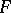 and
and  (that is, separated locally convex topologies
(that is, separated locally convex topologies  on
on 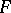 such that the set of all continuous linear functionals on
such that the set of all continuous linear functionals on  endowed with the topology
endowed with the topology 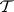 coincides with
coincides with 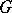 ). The families of sets in
). The families of sets in 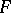 which are bounded relative to the Mackey topology and bounded relative to the weak topology coincide. A convex subsets of
which are bounded relative to the Mackey topology and bounded relative to the weak topology coincide. A convex subsets of  is equicontinuous when
is equicontinuous when 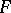 is endowed with the Mackey topology if and only if it is relatively compact in the weak topology. If a separated locally convex space
is endowed with the Mackey topology if and only if it is relatively compact in the weak topology. If a separated locally convex space 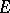 is barrelled or bornological (in particular, metrizable) and
is barrelled or bornological (in particular, metrizable) and 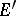 is its dual, then the Mackey topology on
is its dual, then the Mackey topology on 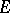 (being dual with
(being dual with 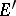 ) coincides with the initial topology on
) coincides with the initial topology on 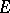 . For pairs of spaces (
. For pairs of spaces (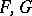 ) in duality the Mackey topology
) in duality the Mackey topology 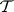 is not necessarily barrelled or metrizable. A weakly-continuous linear mapping of a separated locally convex space
is not necessarily barrelled or metrizable. A weakly-continuous linear mapping of a separated locally convex space 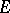 into a separated locally convex space
into a separated locally convex space 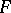 is continuous relative to the Mackey topologies
is continuous relative to the Mackey topologies 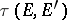 and
and 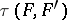 . A locally convex space
. A locally convex space 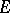 is called a Mackey space if the topology on
is called a Mackey space if the topology on 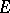 is
is 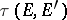 . Completions, quotient spaces and metrizable subspaces, products, locally convex direct sums, and inductive limits of families of Mackey spaces are Mackey spaces. If
. Completions, quotient spaces and metrizable subspaces, products, locally convex direct sums, and inductive limits of families of Mackey spaces are Mackey spaces. If 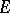 is a Mackey space and
is a Mackey space and 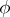 is a weakly-continuous mapping of
is a weakly-continuous mapping of 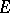 into a locally convex space
into a locally convex space 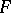 , then
, then 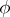 is a continuous linear mapping of
is a continuous linear mapping of 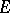 into
into 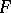 . If
. If 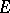 is a quasi-complete Mackey space and the space dual to
is a quasi-complete Mackey space and the space dual to 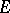 equipped with the strong
equipped with the strong 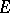 -topology is semi-reflexive, then
-topology is semi-reflexive, then 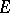 is reflexive.
is reflexive.
References
| [1] | G.W. Mackey, "On convex topological linear spaces" Trans. Amer. Math. Soc. , 60 (1946) pp. 519–537 |
| [2] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) |
| [3] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
Comments
References
| [a1] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) |
Mackey topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mackey_topology&oldid=13416