MacWilliams identities
A  -dimensional subspace
-dimensional subspace  of the linear space
of the linear space  of all
of all  -tuples over the finite field
-tuples over the finite field  is called an
is called an  linear code over
linear code over  . The vectors in
. The vectors in  are called code words. The weight of a vector is the number of its non-zero components. A generator matrix for a code
are called code words. The weight of a vector is the number of its non-zero components. A generator matrix for a code 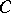 is any
is any 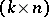 -matrix
-matrix 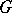 whose rows form a basis of
whose rows form a basis of 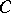 . The ordinary inner product of vectors
. The ordinary inner product of vectors 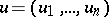 ,
, 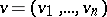 in
in 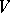 is
is
 |
The dual of 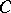 is the
is the 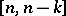 linear code
linear code 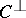 defined by
defined by
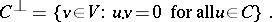 |
The weight distribution of a code 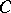 of length
of length  gives the number of vectors of each weight
gives the number of vectors of each weight 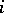 ,
, 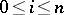 , denoted by
, denoted by 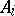 . For example, let
. For example, let 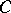 be the
be the  linear code over
linear code over 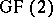 with generating matrix
with generating matrix
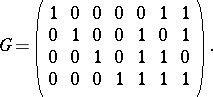 |
The only non-zero weights in 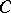 are
are 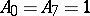 ,
, 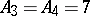 .
.
While the weight distribution does not, in general, uniquely determine a code, it gives important information that has both practical and theoretical significance. The most fundamental result about weight distributions are the MacWilliams equations, a set of linear relations between the weight distributions of 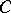 and
and 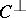 . These equations imply that the weight distribution of
. These equations imply that the weight distribution of 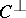 is uniquely determined by the weight distribution of
is uniquely determined by the weight distribution of 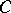 . These relations have been the most significant tool available for investigating and calculating weight distributions.
. These relations have been the most significant tool available for investigating and calculating weight distributions.
Let 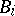 denote the number of vectors of weight
denote the number of vectors of weight 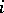 in
in 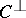 . If
. If 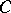 is an
is an 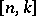 linear code over
linear code over 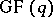 , then there are two equivalent sets of MacWilliams equations [a1]:
, then there are two equivalent sets of MacWilliams equations [a1]:
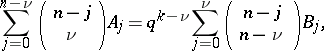 | (a1) |
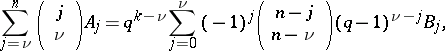 | (a2) |
where  .
.
If 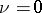 , both sets of equations say that
, both sets of equations say that 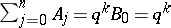 , which states the obvious result that an
, which states the obvious result that an 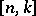 code over
code over 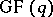 contains
contains 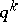 codewords. The other equations are not so obvious. One can solve either set of equations for the weight distribution of
codewords. The other equations are not so obvious. One can solve either set of equations for the weight distribution of 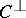 , obtaining
, obtaining 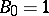 and
and 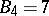 .
.
An elegant and much used way to express these relations is in terms of polynomials. The weight enumerator of a code 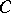 of length
of length  is:
is:
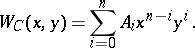 |
The following equation is equivalent to either (a1) or (a2) for a code  over
over 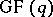 :
:
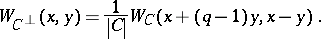 | (a3) |
Two other sets of equations equivalent to either (a1), (a2) or (a3) and more convenient for some calculations are called the power moment identities [a3]. They involve the Stirling numbers of the second kind 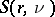 (cf. also Combinatorial analysis). One such set is
(cf. also Combinatorial analysis). One such set is
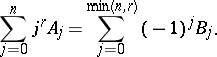 | (a4) |
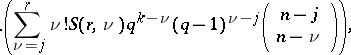 |
where 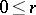 .
.
The power moments are particularly useful for giving conditions under which the weight distributions of a code and its dual are uniquely determined. This is illustrated in the following theorem: A unique solution to the power moments exists under the conditions that  or fewer
or fewer 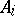 's are unknown and that
's are unknown and that 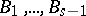 are known [a3]. In this situation, the weight distributions of both
are known [a3]. In this situation, the weight distributions of both 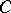 and
and 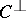 are uniquely determined.
are uniquely determined.
There are also MacWilliams equations for non-linear codes [a2].
References
| [a1] | F.J. MacWilliams, "A theorem on the distribution of weights in a systematic code" Bell System Techn. J. , 42 (1963) pp. 79–94 |
| [a2] | F.J. MacWilliams, N.J.A. Sloane, J.M. Goethals, "The MacWilliams identities for nonlinear codes" Bell System Techn. J. , 51 (1972) pp. 803–819 |
| [a3] | V. Pless, "Power moment identities on weight distributions in error-correcting codes" Inform. and Control , 6 (1963) pp. 147–152 |
MacWilliams identities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=MacWilliams_identities&oldid=16837