M-estimator
A generalization of the maximum-likelihood estimator (MLE) in mathematical statistics (cf. also Maximum-likelihood method; Statistical estimator). Suppose one has univariate observations  which are independent and identically distributed according to a distribution
which are independent and identically distributed according to a distribution 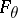 with univariate parameter
with univariate parameter 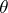 . Denote by
. Denote by 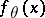 the likelihood of
the likelihood of 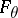 . The maximum-likelihood estimator is defined as the value
. The maximum-likelihood estimator is defined as the value 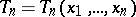 which maximizes
which maximizes 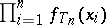 . If
. If  for all
for all  and
and 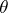 , then this is equivalent to minimizing
, then this is equivalent to minimizing 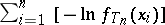 . P.J. Huber [a1] has generalized this to M-estimators, which are defined by minimizing
. P.J. Huber [a1] has generalized this to M-estimators, which are defined by minimizing 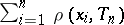 , where
, where 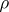 is an arbitrary real function. When
is an arbitrary real function. When 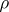 has a partial derivative
has a partial derivative 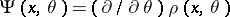 , then
, then  satisfies the implicit equation
satisfies the implicit equation
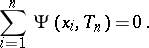 |
Note that the maximum-likelihood estimator is an M-estimator, obtained by putting  .
.
The maximum-likelihood estimator can give arbitrarily bad results when the underlying assumptions (e.g., the form of the distribution generating the data) are not satisfied (e.g., because the data contain some outliers, cf. also Outlier). M-estimators are particularly useful in robust statistics, which aims to construct methods that are relatively insensitive to deviations from the standard assumptions. M-estimators with bounded 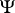 are typically robust.
are typically robust.
Apart from the finite-sample version 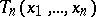 of the M-estimator, there is also a functional version
of the M-estimator, there is also a functional version 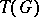 defined for any probability distribution
defined for any probability distribution 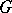 by
by
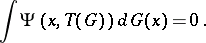 |
Here, it is assumed that 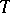 is Fisher-consistent, i.e. that
is Fisher-consistent, i.e. that 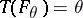 for all
for all 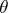 . The influence function of a functional
. The influence function of a functional 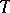 in
in 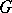 is defined, as in [a2], by
is defined, as in [a2], by
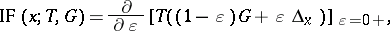 |
where 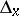 is the probability distribution which puts all its mass in the point
is the probability distribution which puts all its mass in the point  . Therefore
. Therefore 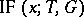 describes the effect of a single outlier in
describes the effect of a single outlier in  on the estimator
on the estimator 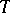 . For an M-estimator
. For an M-estimator 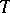 at
at 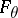 ,
,
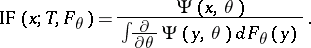 |
The influence function of an M-estimator is thus proportional to 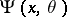 itself. Under suitable conditions, [a3], M-estimators are asymptotically normal with asymptotic variance
itself. Under suitable conditions, [a3], M-estimators are asymptotically normal with asymptotic variance  .
.
Optimal robust M-estimators can be obtained by solving Huber's minimax variance problem [a1] or by minimizing the asymptotic variance 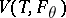 subject to an upper bound on the gross-error sensitivity
subject to an upper bound on the gross-error sensitivity 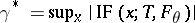 as in [a2].
as in [a2].
When estimating a univariate location, it is natural to use 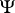 -functions of the type
-functions of the type 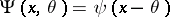 . The optimal robust M-estimator for univariate location at the Gaussian location model
. The optimal robust M-estimator for univariate location at the Gaussian location model 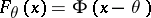 (cf. also Gauss law) is given by
(cf. also Gauss law) is given by 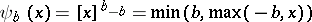 . This
. This  has come to be known as Huber's function. Note that when
has come to be known as Huber's function. Note that when 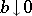 , this M-estimator tends to the median (cf. also Median (in statistics)), and when
, this M-estimator tends to the median (cf. also Median (in statistics)), and when 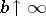 it tends to the mean (cf. also Average).
it tends to the mean (cf. also Average).
The breakdown value 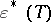 of an estimator
of an estimator 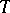 is the largest fraction of arbitrary outliers it can tolerate without becoming unbounded (see [a2]). Any M-estimator with a monotone and bounded
is the largest fraction of arbitrary outliers it can tolerate without becoming unbounded (see [a2]). Any M-estimator with a monotone and bounded 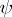 function has breakdown value
function has breakdown value 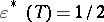 , the highest possible value.
, the highest possible value.
Location M-estimators are not invariant with respect to scale. Therefore it is recommended to compute 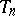 from
from
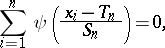 | (a1) |
where 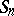 is a robust estimator of scale, e.g. the median absolute deviation
is a robust estimator of scale, e.g. the median absolute deviation
 |
which has  .
.
For univariate scale estimation one uses 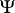 -functions of the type
-functions of the type 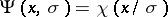 . At the Gaussian scale model
. At the Gaussian scale model 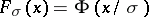 , the optimal robust M-estimators are given by
, the optimal robust M-estimators are given by 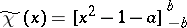 . For
. For 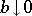 one obtains the median absolute deviation and for
one obtains the median absolute deviation and for 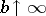 the standard deviation. In the general case, where both location and scale are unknown, one first computes
the standard deviation. In the general case, where both location and scale are unknown, one first computes 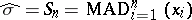 and then plugs it into (a1) for finding
and then plugs it into (a1) for finding  .
.
For multivariate location and scatter matrices, M-estimators were defined by R.A. Maronna [a4], who also gave their influence function and asymptotic covariance matrix. For 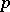 -dimensional data, the breakdown value of M-estimators is at most
-dimensional data, the breakdown value of M-estimators is at most 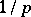 .
.
For regression analysis, one considers the linear model 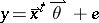 where
where 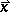 and
and 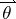 are column vectors, and
are column vectors, and 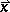 and the error term
and the error term  are independent. Let
are independent. Let  have a distribution with location zero and scale
have a distribution with location zero and scale  . For simplicity, put
. For simplicity, put 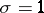 . Denote by
. Denote by 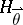 the joint distribution of
the joint distribution of 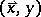 , which implies the distribution of the error term
, which implies the distribution of the error term 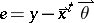 . Based on a data set
. Based on a data set 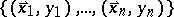 , M-estimators
, M-estimators 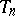 for regression [a3] are defined by
for regression [a3] are defined by
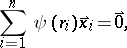 |
where 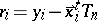 are the residuals. If the Huber function
are the residuals. If the Huber function 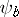 is used, the influence function of
is used, the influence function of 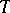 at
at 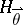 equals
equals
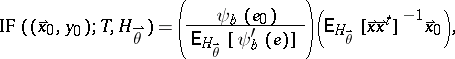 | (a2) |
where 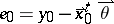 . The first factor of (a2) is the influence of the vertical error
. The first factor of (a2) is the influence of the vertical error 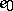 . It is bounded, which makes this estimator more robust than least squares (cf. also Least squares, method of). The second factor is the influence of the position
. It is bounded, which makes this estimator more robust than least squares (cf. also Least squares, method of). The second factor is the influence of the position 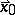 . Unfortunately, this factor is unbounded, hence a single outlying
. Unfortunately, this factor is unbounded, hence a single outlying 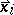 (i.e., a horizontal outlier) will almost completely determine the fit, as shown in [a2]. Therefore the breakdown value
(i.e., a horizontal outlier) will almost completely determine the fit, as shown in [a2]. Therefore the breakdown value 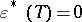 .
.
To obtain a bounded influence function, generalized M-estimators [a2] are defined by
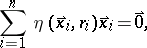 |
for some real function 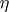 . The influence function of
. The influence function of 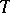 at
at 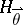 now becomes
now becomes
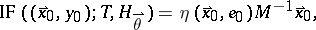 | (a3) |
where 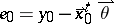 and
and 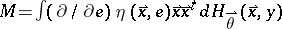 . For an appropriate choice of the function
. For an appropriate choice of the function 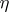 , the influence function (a3) is bounded, but still the breakdown value
, the influence function (a3) is bounded, but still the breakdown value 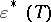 goes down to zero when the number of parameters
goes down to zero when the number of parameters 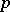 increases.
increases.
To repair this, P.J. Rousseeuw and V.J. Yohai [a5] have introduced S-estimators. An S-estimator 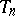 minimizes
minimizes 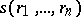 , where
, where  are the residuals and
are the residuals and 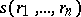 is the robust scale estimator defined as the solution of
is the robust scale estimator defined as the solution of
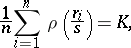 |
where 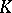 is taken to be
is taken to be 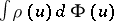 . The function
. The function 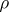 must satisfy
must satisfy 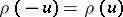 and
and 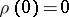 and be continuously differentiable, and there must be a constant
and be continuously differentiable, and there must be a constant 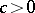 such that
such that 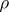 is strictly increasing on
is strictly increasing on 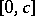 and constant on
and constant on 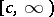 . Any S-estimator has breakdown value
. Any S-estimator has breakdown value 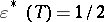 in all dimensions, and it is asymptotically normal with the same asymptotic covariance as the M-estimator with that function
in all dimensions, and it is asymptotically normal with the same asymptotic covariance as the M-estimator with that function 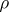 . The S-estimators have also been generalized to multivariate location and scatter matrices, in [a6], and they enjoy the same properties.
. The S-estimators have also been generalized to multivariate location and scatter matrices, in [a6], and they enjoy the same properties.
References
| [a1] | P.J. Huber, "Robust estimation of a location parameter" Ann. Math. Stat. , 35 (1964) pp. 73–101 |
| [a2] | F.R. Hampel, E.M. Ronchetti, P.J. Rousseeuw, W.A. Stahel, "Robust statistics: The approach based on influence functions" , Wiley (1986) |
| [a3] | P.J. Huber, "Robust statistics" , Wiley (1981) |
| [a4] | R.A. Maronna, "Robust M-estimators of multivariate location and scatter" Ann. Statist. , 4 (1976) pp. 51–67 |
| [a5] | P.J. Rousseeuw, V.J. Yohai, "Robust regression by means of S-estimators" J. Franke (ed.) W. Härdle (ed.) R.D. Martin (ed.) , Robust and Nonlinear Time Ser. Analysis , Lecture Notes Statistics , 26 , Springer (1984) pp. 256–272 |
| [a6] | P.J. Rousseeuw, A. Leroy, "Robust regression and outlier detection" , Wiley (1987) |
M-estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M-estimator&oldid=12651