Lyusternik-Shnirel'man-Borsuk covering theorem
A theorem usually stated as follows:
1) Each closed covering  of
of  contains at least one set
contains at least one set  with
with  .
.
Contrary to the equivalent Borsuk–Ulam theorem, it seems to be not common to use the same name also for the following equivalent symmetric versions:
2) Let  be closed sets with
be closed sets with 
 . If
. If  , then
, then  .
.
3) 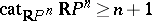 [a2].
[a2].
In all these results, the estimates are optimal (in 3), in fact, equality holds). It is worth mentioning that 2) gave the motivation for the notion of the genus of a set symmetric with respect to a free  -action.
-action.
For other equivalent versions and for generalizations to coverings involving other symmetries (e.g. with respect to free 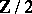 -actions), cf. [a3] and the references therein.
-actions), cf. [a3] and the references therein.
One major field of applications are estimates of the number of critical points of even functionals; this can be used, e.g., in the theory of differential equations.
References
| [a1] | K. Borsuk, "Drei Sätze über die  —dimensionale Sphäre" Fund. Math. , 20 (1933) pp. 177–190 —dimensionale Sphäre" Fund. Math. , 20 (1933) pp. 177–190 |
| [a2] | L. Lyusternik, L. Shnirel'man, "Topological methods in variational problems" , Issl. Inst. Mat. Mekh. OMGU (1930) (In Russian) |
| [a3] | H. Steinlein, "Spheres and symmetry: Borsuk's antipodal theorem" Topol. Methods Nonlinear Anal. , 1 (1993) pp. 15–33 |
Lyusternik-Shnirel'man-Borsuk covering theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyusternik-Shnirel%27man-Borsuk_covering_theorem&oldid=18675