Lyapunov surfaces and curves
A class of surfaces and curves that have quite good smoothness properties; it was introduced in potential theory by A.M. Lyapunov at the turn into the 20th century.
A surface 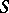 in the three-dimensional Euclidean space
in the three-dimensional Euclidean space 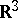 is called a Lyapunov surface if it satisfies the following three conditions (Lyapunov's conditions): 1) at every point of
is called a Lyapunov surface if it satisfies the following three conditions (Lyapunov's conditions): 1) at every point of  there is a well-defined tangent plane, and consequently a well-defined normal; 2) there is a number
there is a well-defined tangent plane, and consequently a well-defined normal; 2) there is a number 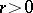 , the same for all points of
, the same for all points of 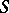 , such that if one takes the part
, such that if one takes the part  of
of 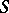 lying inside the Lyapunov sphere
lying inside the Lyapunov sphere 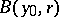 with centre at an arbitrary point
with centre at an arbitrary point 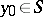 and radius
and radius  , then the lines parallel to the normal to
, then the lines parallel to the normal to 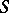 at
at 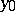 meet
meet 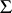 at most once; and 3) there are two numbers
at most once; and 3) there are two numbers 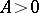 and
and 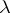 ,
, 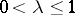 , the same for the whole of
, the same for the whole of  , such that for any two points
, such that for any two points 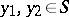 ,
,
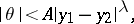 | (*) |
where 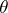 is the angle between the normals to
is the angle between the normals to 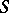 at
at 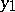 and
and  . Sometimes these three conditions are supplemented by the requirement that
. Sometimes these three conditions are supplemented by the requirement that 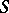 is closed and that the solid angle under which any part
is closed and that the solid angle under which any part 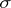 of
of 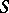 is visible at an arbitrary point
is visible at an arbitrary point 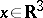 is uniformly bounded.
is uniformly bounded.
The Lyapunov conditions can be generalized to hypersurfaces in 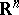 ,
,  .
.
Similarly, a simple continuous curve 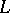 in the plane
in the plane 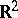 is called a Lyapunov curve if it satisfies the following conditions:
is called a Lyapunov curve if it satisfies the following conditions: 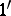 ) at every point of
) at every point of 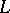 there is a well-defined tangent, and consequently a well-defined normal; and
there is a well-defined tangent, and consequently a well-defined normal; and 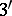 ) there are two numbers
) there are two numbers  and
and 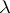 ,
, 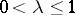 , the same for the whole of
, the same for the whole of 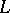 , such that for any two points
, such that for any two points 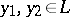 (*) holds, where
(*) holds, where  is the angle between the tangents or normals to
is the angle between the tangents or normals to 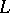 at
at 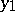 and
and 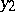 . Here Lyapunov's condition 2) follows from
. Here Lyapunov's condition 2) follows from  ) and
) and 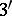 ). The Lyapunov curves are a subclass of the simple smooth curves.
). The Lyapunov curves are a subclass of the simple smooth curves.
References
| [1] | A.M. Lyapunov, "On certain questions connected with the Dirichlet problem" , Collected works , 1 , Moscow (1954) pp. 45–47; 48–100 (In Russian) |
| [2] | S.L. Sobolev, "Partial differential equations of mathematical physics" , Pergamon (1964) (Translated from Russian) |
| [3] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) pp. Chapt. 5 (Translated from Russian) |
| [4] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) pp. Chapt. 1 (Translated from Russian) |
Comments
A Lyapunov surface is necessarily 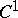 , and on the other hand a compact surface of class
, and on the other hand a compact surface of class 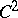 is a Lyapunov surface. Lyapunov surfaces are used in the study of simple- and double-layer potentials.
is a Lyapunov surface. Lyapunov surfaces are used in the study of simple- and double-layer potentials.
Lyapunov surfaces and curves. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyapunov_surfaces_and_curves&oldid=14936