Lyapunov equation
Usually, the matrix equation
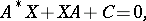 | (a1) |
where the star denotes transposition for matrices with real entries and transposition and complex conjugation for matrices with complex entries; 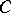 is symmetric (or Hermitian in the complex case; cf. Hermitian matrix; Symmetric matrix). In fact, this is a special case of the matrix Sylvester equation
is symmetric (or Hermitian in the complex case; cf. Hermitian matrix; Symmetric matrix). In fact, this is a special case of the matrix Sylvester equation
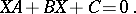 | (a2) |
The main result concerning the Sylvester equation is the following: If 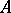 and
and 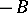 have no common eigenvalues, then the Sylvester equation has a unique solution for any
have no common eigenvalues, then the Sylvester equation has a unique solution for any 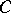 .
.
When 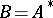 and there are no eigenvalues
and there are no eigenvalues 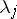 of
of 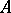 such that
such that 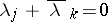 whatever
whatever 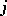 and
and 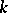 are (in the numbering of eigenvalues of
are (in the numbering of eigenvalues of 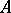 ), then (a1) has a unique Hermitian solution for any
), then (a1) has a unique Hermitian solution for any 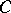 . Moreover if
. Moreover if 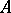 is a Hurwitz matrix (i.e. having all its eigenvalues in the left half-plane, thus having strictly negative real parts), then this unique solution is
is a Hurwitz matrix (i.e. having all its eigenvalues in the left half-plane, thus having strictly negative real parts), then this unique solution is
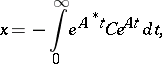 | (a3) |
and if 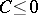 , then
, then 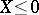 . From this one may deduce that if
. From this one may deduce that if 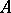 and
and 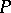 satisfy
satisfy 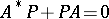 , than a necessary and sufficient condition for
, than a necessary and sufficient condition for  to be a Hurwitz matrix is that
to be a Hurwitz matrix is that 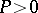 . In fact, this last property justifies the assignment of Lyapunov's name to (a1); in Lyapunov's famous monograph [a1], Chap. 20, Thm. 2, one finds the following result: Consider the partial differential equation
. In fact, this last property justifies the assignment of Lyapunov's name to (a1); in Lyapunov's famous monograph [a1], Chap. 20, Thm. 2, one finds the following result: Consider the partial differential equation
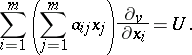 | (a4) |
If 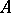 has eigenvalues with strictly negative real parts and
has eigenvalues with strictly negative real parts and 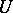 is a form of definite sign and even degree, then the solution,
is a form of definite sign and even degree, then the solution, 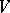 , of this equation will be a form of the same degree that is sign definite (with sign opposite to that of
, of this equation will be a form of the same degree that is sign definite (with sign opposite to that of 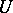 . Now, if
. Now, if 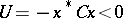 with
with 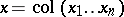 , then
, then 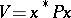 , with
, with 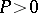 , is a solution of (a1). In fact,
, is a solution of (a1). In fact, 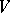 is a Lyapunov function for the system
is a Lyapunov function for the system
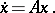 | (a5) |
These facts and results have a straightforward extension to the discrete-time case: for the system
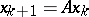 | (a6) |
one may consider the quadratic Lyapunov function as above (i.e. 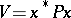 ) and obtain that
) and obtain that 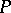 has to be a solution of the discrete-time Lyapunov equation
has to be a solution of the discrete-time Lyapunov equation
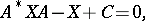 | (a7) |
whose solution has the form
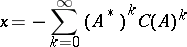 | (a8) |
provided the eigenvalues of 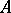 are inside the unit disc.
are inside the unit disc.
The equation may be defined for the time-varying case also. For the system
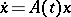 | (a9) |
one may consider the quadratic Lyapunov function 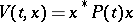 and obtain that
and obtain that 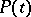 has to be the unique solution, bounded on the whole real axis, of the matrix differential equation
has to be the unique solution, bounded on the whole real axis, of the matrix differential equation
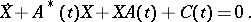 | (a10) |
This solution is
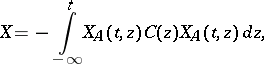 | (a11) |
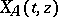 being the matrix solution of
being the matrix solution of 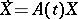 ,
, 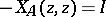 . The solution is well defined if
. The solution is well defined if 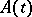 defines an exponentially stable evolution (
defines an exponentially stable evolution (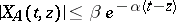 ,
, 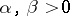 ). It is worth mentioning that if
). It is worth mentioning that if 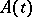 and
and 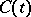 are periodic or almost periodic, then
are periodic or almost periodic, then 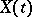 defined by (a11) is periodic or almost periodic, respectively. Extensions of this result to a discrete-time or infinite dimensional (operator) case are widely known. Actually, the Lyapunov equation has many applications in stability and control theory; efficient numerical algorithms for solving it are available.
defined by (a11) is periodic or almost periodic, respectively. Extensions of this result to a discrete-time or infinite dimensional (operator) case are widely known. Actually, the Lyapunov equation has many applications in stability and control theory; efficient numerical algorithms for solving it are available.
References
| [a1] | A.M. Lyapunov, "General problem of stability of motion" , USSR Acad. Publ. House (1950) (In Russian) |
| [a2] | R.E. Bellman, "Introduction to matrix-analysis" , McGraw-Hill (1960) |
| [a3] | A. Halanay, "Differential equations: stability, oscillations time lags" , Acad. Press (1966) |
| [a4] | A. Halanay, D. Wexler, "Qualitative theory of pulse systems" , Nauka (1971) (In Russian) |
| [a5] | A. Halanay, V. Räsvan, "Applications of Lyapunov methods in stability" , Kluwer Acad. Publ. (1993) |
Lyapunov equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyapunov_equation&oldid=15487