Lyapunov characteristic exponent
of a solution of a linear system
The limes superior
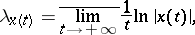 |
where 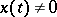 is a solution of the linear system of ordinary differential equations
is a solution of the linear system of ordinary differential equations
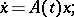 | (1) |
here  and
and 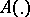 is a mapping
is a mapping 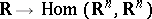 , summable on every interval. In coordinates,
, summable on every interval. In coordinates,
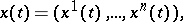 |
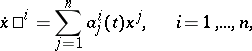 |
where 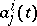 are functions summable on every interval and
are functions summable on every interval and
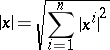 |
(or any other equivalent norm; 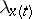 does not depend on the choice of the norm in
does not depend on the choice of the norm in 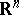 or in
or in 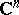 ).
).
Lyapunov's theorem. Suppose that
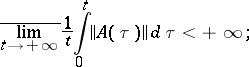 |
equivalently:
 |
Then for any solution 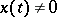 of the system (1) the Lyapunov characteristic exponent
of the system (1) the Lyapunov characteristic exponent 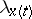 is a real number (that is,
is a real number (that is, 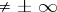 ). The following assertions hold for the Lyapunov characteristic exponents of non-zero solutions of (1):
). The following assertions hold for the Lyapunov characteristic exponents of non-zero solutions of (1):
1) 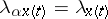 ,
, 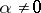 ;
;
2) 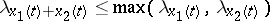 ;
;
3) there exists a set of linearly independent solutions of (1), denoted by 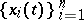 , such that for any other
, such that for any other  linearly independent solutions
linearly independent solutions 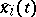 ,
, 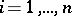 , of (1), numbered in decreasing order of the Lyapunov characteristic exponents, that is,
, of (1), numbered in decreasing order of the Lyapunov characteristic exponents, that is, 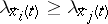 for
for 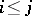 , the following inequalities hold:
, the following inequalities hold:
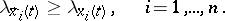 |
A fundamental system of solutions 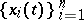 with this property is called normal. Such a normal system has the properties:
with this property is called normal. Such a normal system has the properties:
a) the family of numbers 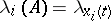 ,
, 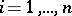 , does not depend on the choice of the normal fundamental system;
, does not depend on the choice of the normal fundamental system;
b) for any solution 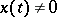 of (1) its Lyapunov characteristic exponent
of (1) its Lyapunov characteristic exponent 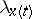 is equal to some
is equal to some 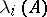 ;
;
c) 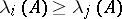 ,
, 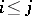 .
.
The numbers 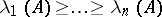 are called the Lyapunov characteristic exponents of the system (1); the number
are called the Lyapunov characteristic exponents of the system (1); the number 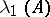 is often called the leading Lyapunov characteristic exponent of (1).
is often called the leading Lyapunov characteristic exponent of (1).
The set of all Lyapunov characteristic exponents of non-zero solutions of (1) is called the spectrum.
Special case.
1) A system with constant coefficients (that is, 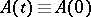 ). In this case the
). In this case the 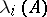 are equal to the real parts of the eigen values of the operator
are equal to the real parts of the eigen values of the operator 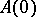 (the matrix
(the matrix 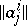 ).
).
2) A system with periodic coefficients (that is, 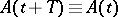 ,
, 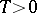 ). In this case
). In this case
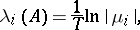 |
where 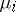 are the multipliers of the system (1), numbered in non-increasing order of their moduli (each is taken as many times as its multiplicity).
are the multipliers of the system (1), numbered in non-increasing order of their moduli (each is taken as many times as its multiplicity).
The role of the Lyapunov characteristic exponent in the theory of Lyapunov stability is based on the following assertion: If  (
(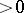 ), then the solutions of (1) are asymptotically stable (respectively, unstable, cf. Asymptotically-stable solution). From
), then the solutions of (1) are asymptotically stable (respectively, unstable, cf. Asymptotically-stable solution). From 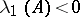 it does not follow that the null solution of the system
it does not follow that the null solution of the system
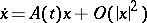 |
is Lyapunov stable; however, if it is also known that the system (1) is a regular linear system, then this conclusion is valid (Lyapunov's theorem).
Suppose that the system 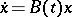 is obtained by a small perturbation of a system (1) satisfying the condition
is obtained by a small perturbation of a system (1) satisfying the condition
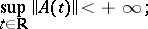 |
that is, the distance between them, defined by the formula
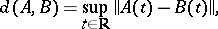 | (2) |
is small. For 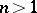 this does not imply that the quantity
this does not imply that the quantity
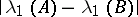 |
is small (it is implied if the system (1) has constant or periodic coefficients, and also for certain other systems); in other words, the functionals 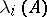 are not everywhere continuous on the space of systems (1) (
are not everywhere continuous on the space of systems (1) (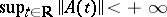 ), endowed with the given metric (2).
), endowed with the given metric (2).
Lyapunov characteristic exponents were introduced by A.M. Lyapunov, not only for solutions of the system (1), but also for arbitrary functions on  (see [1]).
(see [1]).
References
| [1] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [2] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [3] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
Comments
Presently, Lyapunov (characteristic) exponents are used at a much wider scale. For a survey see [a6]. First, the matrix A may be a stochastic time-dependent function. Lyapunov exponents are also used in relation with a system of non-linear differential equations
 |
having a strange attractor (or repellor) 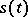 as limit solution, see [a7]. The system linearized in
as limit solution, see [a7]. The system linearized in 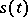 is of the form (1) with
is of the form (1) with
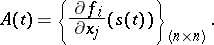 |
One of the exponents is zero. The occurrence of one or more positive exponents indicates that 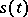 is a strange attractor. For a conservative system the sum of the Lyapunov exponents is zero, while for a dissipative system the sum is negative. The capacity
is a strange attractor. For a conservative system the sum of the Lyapunov exponents is zero, while for a dissipative system the sum is negative. The capacity  of a strange attractor is a fractal number related to the Hausdorff dimension. J.L. Kaplan and J.A. Yorke made the conjecture
of a strange attractor is a fractal number related to the Hausdorff dimension. J.L. Kaplan and J.A. Yorke made the conjecture
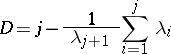 |
with 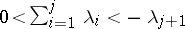 (
(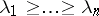 ).
).
The concept of Lyapunov exponents extends to non-linear stochastic systems, as well as to iteration mappings
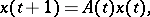 |
In a yet more general deterministic setting, let 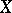 be a compact subset of a Hilbert space
be a compact subset of a Hilbert space 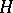 , and let
, and let 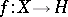 be a mapping such that
be a mapping such that 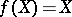 . The mapping
. The mapping 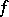 is supposed to satisfy the following uniform differentiability condition: For each
is supposed to satisfy the following uniform differentiability condition: For each 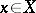 there is a linear compact operator
there is a linear compact operator 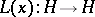 such that
such that
 |
as  , where
, where  denotes the norm in
denotes the norm in 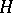 , and where the supremum is taken over all
, and where the supremum is taken over all 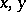 with
with 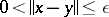 .
.
For a compact linear operator 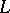 , let
, let 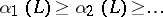 be the eigen values of
be the eigen values of 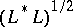 . For each positive integer
. For each positive integer  , let
, let 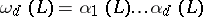 , while for a non-integer positive real number
, while for a non-integer positive real number 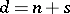 ,
, 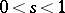 , define
, define 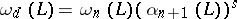 .
.
Suppose that 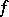 and
and 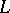 are such that
are such that 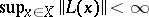 .
.
For each 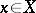 , let
, let 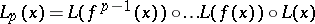 , where
, where 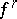 denotes the
denotes the  -th iterate of
-th iterate of 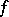 . Define the (local) Lyapunov numbers and Lyapunov exponents by
. Define the (local) Lyapunov numbers and Lyapunov exponents by
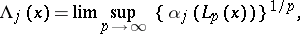 |
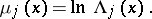 |
The uniform Lyapunov exponents 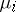 and uniform Lyapunov numbers
and uniform Lyapunov numbers 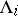 in this setting are defined as follows:
in this setting are defined as follows:
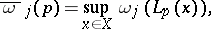 |
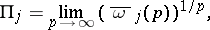 |
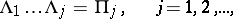 |
 |
Let  be the smallest integer such that
be the smallest integer such that 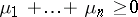 and
and 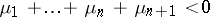 . The number
. The number 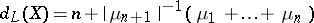 is then called the Lyapunov dimension of
is then called the Lyapunov dimension of 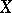 . One has (see [a2])
. One has (see [a2]) 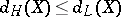 , where
, where  is the Hausdorff dimension of
is the Hausdorff dimension of 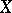 .
.
References
| [a1] | W. Kliemann, "Analysis of nonlinear stochastic systems" W. Schiehlen (ed.) W. Wedig (ed.) , Analysis and estimation of stochastic mechanical systems , Springer (Wien) (1988) pp. 43–102 |
| [a2] | P. Constantin, C. Foias, R. Temam, "Attractors representing turbulent flows" , Amer. Math. Soc. (1985) |
| [a3] | L.S. Young, "Capacity of attractors" Ergod. Th. Dynam. Systems , 1 (1981) pp. 381–383 |
| [a4] | L.S. Young, "Dimension, entropy, and Lyapunov exponents" Ergod. Th. Dynam. Systems , 2 (1982) pp. 109–124 |
| [a5] | P. Fredrickson, J.L. Kaplan, E.D. Yorke, J.A. Yorke, "The Lyapunov dimension of strange attractors" J. Diff. Eq. , 49 (1983) pp. 185–207 |
| [a6] | L. Arnold (ed.) V. Wihstutz (ed.) , Lyapunov exponents , Lect. notes in math. , 1186 , Springer (1986) |
| [a7] | H.G. Schuster, "Deterministic chaos" , Physik-Verlag (1988) |
| [a8] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [a9] | J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983) |
Lyapunov characteristic exponent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyapunov_characteristic_exponent&oldid=12994