Luzin-Privalov theorems
in the theory of functions of a complex variable
Classical results of N.N. Luzin and I.I. Privalov that clarify the character of a boundary uniqueness property of analytic functions (cf. Uniqueness properties of analytic functions) (see [1]).
1) Let 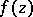 be a meromorphic function of the complex variable
be a meromorphic function of the complex variable  in a simply-connected domain
in a simply-connected domain  with rectifiable boundary
with rectifiable boundary 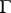 . If
. If 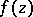 takes angular boundary values zero on a set
takes angular boundary values zero on a set 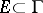 of positive Lebesgue measure on
of positive Lebesgue measure on 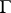 , then
, then 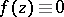 in
in 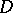 . There is no function meromorphic in
. There is no function meromorphic in 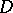 that has infinite angular boundary values on a set
that has infinite angular boundary values on a set 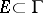 of positive measure.
of positive measure.
2) Let 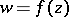 be a meromorphic function in the unit disc
be a meromorphic function in the unit disc 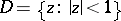 other than a constant and having radial boundary values (finite or infinite) on a set
other than a constant and having radial boundary values (finite or infinite) on a set 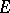 situated on an arc
situated on an arc  of the unit circle
of the unit circle 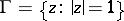 that is metrically dense and of the second Baire category (cf. Baire classes) on
that is metrically dense and of the second Baire category (cf. Baire classes) on 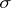 . Then the set
. Then the set 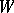 of its radial boundary values on
of its radial boundary values on 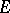 contains at least two distinct points. Metric density of
contains at least two distinct points. Metric density of 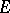 on
on 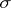 means that every portion of
means that every portion of 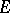 on
on 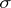 has positive measure. This implies that if the radial boundary values of
has positive measure. This implies that if the radial boundary values of 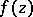 on a set
on a set 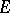 of the given type are equal to zero, then
of the given type are equal to zero, then 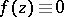 in
in 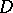 . Moreover, there is no meromorphic function in the unit disc that takes infinite radial boundary values on a set
. Moreover, there is no meromorphic function in the unit disc that takes infinite radial boundary values on a set 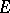 of the given type.
of the given type.
Luzin and Privalov (see [1], [2]) constructed examples to show that neither metric density nor second Baire category are by themselves sufficient for the assertion in 2 to hold.
See also Boundary properties of analytic functions; Luzin examples; Cluster set; Privalov theorem; Riesz theorem.
References
| [1] | N.N. [N.N. Luzin] Lusin, I.I. [I.I. Privalov] Priwaloff, "Sur l'unicité et la multiplicité des fonctions analytiques" Ann. Sci. Ecole Norm. Sup. (3) , 42 (1925) pp. 143–191 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | A. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
Comments
References
| [a1] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
Luzin-Privalov theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luzin-Privalov_theorems&oldid=12447