Logical consequence
of a given set of premises
A proposition that is true for any interpretation of the non-logical symbols (that is, the names (cf. Name) of objects, functions, predicates) for which the premises are true. If a proposition 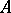 is a logical consequence of a set of propositions
is a logical consequence of a set of propositions 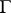 , one says that
, one says that 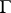 logically implies
logically implies 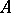 , or that
, or that 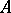 follows logically from
follows logically from 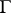 .
.
If 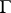 is a set of statements of a formalized first-order logico-mathematical language (cf. Logico-mathematical calculus) and
is a set of statements of a formalized first-order logico-mathematical language (cf. Logico-mathematical calculus) and 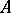 is a proposition of this language, then the relation "A is a logical consequence of G" means that any model for
is a proposition of this language, then the relation "A is a logical consequence of G" means that any model for 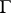 is a model for
is a model for 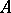 . This relation is denoted by
. This relation is denoted by 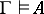 . The Gödel completeness theorem of classical predicate calculus implies that the relation
. The Gödel completeness theorem of classical predicate calculus implies that the relation 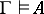 coincides with the relation
coincides with the relation  , that is,
, that is,  if and only if
if and only if  is deducible from
is deducible from 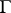 by the methods of classical predicate calculus.
by the methods of classical predicate calculus.
References
| [1] | H. Rasiowa, "The mathematics of metamathematics" , Polska Akad. Nauk (1963) |
| [2] | K. Gödel, "Die Vollständigkeit der Axiome des logischen Funktionenkalküls" Monatsh. Math. Phys. , 37 (1930) pp. 349–360 |
Comments
The phrase "semantic entailmentsemantic entailment" is sometimes used instead of "logical consequence" ; thus, the expression  is read as "G semantically entails A" . The expression
is read as "G semantically entails A" . The expression 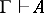 is similarly read as "G syntactically entails A" .
is similarly read as "G syntactically entails A" .
References
| [a1] | P.T. Johnstone, "Notes on logic and set theory" , Cambridge Univ. Press (1987) |
| [a2] | A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974) |
Logical consequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logical_consequence&oldid=19217