Logical axiom
A logical system 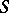 generally consists of a language
generally consists of a language 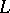 and a set
and a set 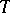 of sentences of
of sentences of  , called provable in
, called provable in 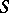 .
. 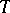 is defined inductively, as being the smallest set of sentences of
is defined inductively, as being the smallest set of sentences of  which contains a given set
which contains a given set  of
of  -sentences and closed under certain specified operations. The elements of
-sentences and closed under certain specified operations. The elements of 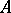 are called the logical axioms of
are called the logical axioms of 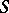 .
.
References
| [1] | E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964) |
| [2] | J.R. Shoenfield, "Mathematical logic" , Addison-Wesley (1967) |
Comments
The phrase "logical axiom" is often more specifically used to distinguish those axioms, in a formal theory, which are concerned with securing the meaning of the logical connectives and quantifiers (cf. Logical calculus), as opposed to the "non-logical axioms" which are the standing hypotheses about the interpretation of the particular function and predicate symbols in the language in which the theory is formulated (cf. Logico-mathematical calculus).
Logical axiom. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logical_axiom&oldid=15648