Logarithmic potential
A potential with the logarithmic kernel 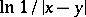 , where
, where 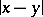 is the distance between the points
is the distance between the points  and
and 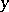 of the Euclidean plane
of the Euclidean plane 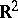 , that is, a potential of the form
, that is, a potential of the form
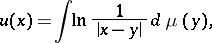 | (1) |
where, generally, speaking, the integration is carried out with respect to an arbitrary Borel measure 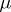 on
on 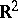 with compact support
with compact support 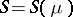 . Physically one can assume that the logarithmic potential arises from the Newton potential of the forces of gravitation when the distribution of the attracting masses in the Euclidean space
. Physically one can assume that the logarithmic potential arises from the Newton potential of the forces of gravitation when the distribution of the attracting masses in the Euclidean space 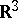 of points
of points 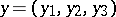 does not depend, for example, on the coordinate
does not depend, for example, on the coordinate 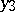 . Of course the total mass is infinite, but if one performs a regularization of the resulting attracting force
. Of course the total mass is infinite, but if one performs a regularization of the resulting attracting force 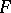 , which can be regarded as acting in the plane
, which can be regarded as acting in the plane 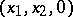 , consisting in discarding the infinite term, then the potential of the finite part of
, consisting in discarding the infinite term, then the potential of the finite part of 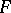 will invariably have the form (1) (see [2]). In contrast to the Newton kernel, the logarithmic kernel has a singularity not only as
will invariably have the form (1) (see [2]). In contrast to the Newton kernel, the logarithmic kernel has a singularity not only as 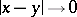 , but also as
, but also as 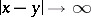 , which causes some differences in the behaviour of the logarithmic potential as compared with the Newton potential. They occur mainly in the solution of exterior boundary value problems (see Exterior and interior boundary value problems). The main applications of the logarithmic potential occur in the solution of planar boundary value problems in potential theory (see also Boundary value problem, elliptic equations).
, which causes some differences in the behaviour of the logarithmic potential as compared with the Newton potential. They occur mainly in the solution of exterior boundary value problems (see Exterior and interior boundary value problems). The main applications of the logarithmic potential occur in the solution of planar boundary value problems in potential theory (see also Boundary value problem, elliptic equations).
The main properties of the logarithmic potential are: 1) outside the support 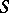 of the measure
of the measure 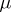 the logarithmic potential is a regular solution of the Laplace equation
the logarithmic potential is a regular solution of the Laplace equation 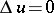 , that is,
, that is,  is a harmonic function on the open set
is a harmonic function on the open set 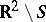 , but is not regular at infinity, however; 2) if the measure
, but is not regular at infinity, however; 2) if the measure 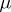 is absolutely continuous, that is, the integral (1) takes the form
is absolutely continuous, that is, the integral (1) takes the form
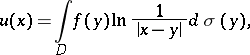 | (2) |
where 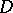 is a finite domain,
is a finite domain, 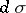 is the area element of
is the area element of 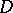 and the density
and the density 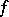 belongs to the class
belongs to the class 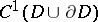 , then the second derivatives of
, then the second derivatives of  are continuous in
are continuous in 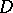 and satisfy the Poisson equation
and satisfy the Poisson equation 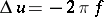 .
.
If the integral in (2) extends along a closed Lyapunov curve 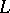 (see Lyapunov surfaces and curves), that is,
(see Lyapunov surfaces and curves), that is,
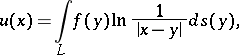 | (3) |
one talks of the logarithmic potential of a single (or simple) layer, distributed on 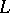 . If
. If 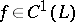 , then the logarithmic potential of the single layer (3) is continuous everywhere in
, then the logarithmic potential of the single layer (3) is continuous everywhere in 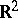 . Its normal derivative has limits from the inside and the outside of
. Its normal derivative has limits from the inside and the outside of 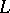 , respectively:
, respectively:
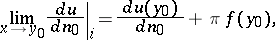 |
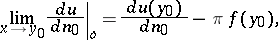 |
where
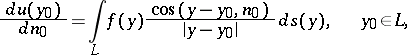 | (4) |
is the so-called direct value of the normal derivative of the logarithmic potential of a single layer and 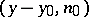 is the angle between the vector
is the angle between the vector 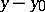 and the outward normal
and the outward normal 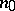 to
to 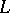 at the point
at the point 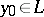 . The integral (4) is continuous on
. The integral (4) is continuous on 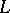 .
.
The logarithmic potential of a double layer has the form
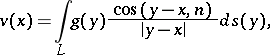 | (5) |
where  is the outward normal to
is the outward normal to 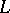 at
at 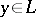 . If
. If 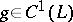 , then the logarithmic potential of the double layer (5) is a regular harmonic function inside and outside
, then the logarithmic potential of the double layer (5) is a regular harmonic function inside and outside 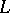 and has normal (non-angular) limits from the inside and the outside of
and has normal (non-angular) limits from the inside and the outside of 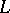 , respectively:
, respectively:
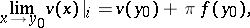 |
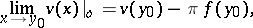 |
where
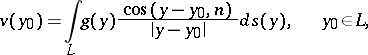 |
is the direct value of the logarithmic potential of the double layer at the point 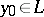 . The normal derivative of the logarithmic potential of a double layer is continuous under transition through
. The normal derivative of the logarithmic potential of a double layer is continuous under transition through 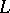 .
.
The listed boundary properties of the logarithmic potential of a simple and a double layer are completely analogous to the corresponding properties of the Newton potential (see also Potential theory). From (5) it is obvious that the logarithmic potential of a double layer is a harmonic function that is regular at infinity.
The logarithmic potential is also directly connected with boundary value problems of analytic function theory, since an integral of Cauchy type can be expressed in terms of the logarithmic potential of a single and a double layer (see [3]).
References
| [1] | S.L. Sobolev, "Partial differential equations of mathematical physics" , Pergamon (1964) (Translated from Russian) |
| [2] | A.G. Webster, "Partial differential equations of mathematical physics" , Hafner (1955) |
| [3] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [4] | Ch.J. de la Vallée-Poussin, "Le potentiel logarithmique, balayage et répresentation conforme" , Libraire Univ. Louvain (1949) |
| [5] | G.C. Evans, "The logarithmic potential, discontinuous Dirichlet and Neumann problems" , New York (1927) |
Comments
See also Lyapunov theorem.
References
| [a1] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) |
| [a2] | J. Král, "Integral operators in potential theory" , Lect. notes in math. , 823 , Springer (1980) |
Logarithmic potential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_potential&oldid=11977