Logarithmic function
logarithm
The function inverse to the exponential function. The logarithmic function is denoted by
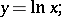 | (1) |
its value  , corresponding to the value of the argument
, corresponding to the value of the argument  , is called the natural logarithm of
, is called the natural logarithm of  . From the definition, relation (1) is equivalent to
. From the definition, relation (1) is equivalent to
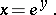 | (2) |
Since  for any real
for any real  , the logarithmic function is defined only for
, the logarithmic function is defined only for  . In a more general sense a logarithmic function is a function
. In a more general sense a logarithmic function is a function
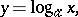 |
where  (
( ) is an arbitrary base of the logarithm; this function can be expressed in terms of
) is an arbitrary base of the logarithm; this function can be expressed in terms of  by the formula
by the formula
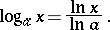 |
The logarithmic function is one of the main elementary functions; its graph (see Fig.) is called a logarithmic curve.

Figure: l060600a
The main properties of the logarithmic function follow from the corresponding properties of the exponential function and logarithms; for example, the logarithmic function satisfies the functional equation
 |
The logarithmic function  is a strictly-increasing function, and
is a strictly-increasing function, and 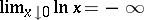 ,
,  . At every point
. At every point  the logarithmic function has derivatives of all orders and in a sufficiently small neighbourhood it can be expanded in a power series, that is, it is an analytic function. For
the logarithmic function has derivatives of all orders and in a sufficiently small neighbourhood it can be expanded in a power series, that is, it is an analytic function. For  the following expansion of the (natural) logarithmic function is valid:
the following expansion of the (natural) logarithmic function is valid:
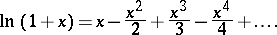 |
The derivative of the logarithmic function is
 |
Many integrals can be expressed in terms of the logarithmic function; for example:
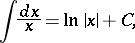 |
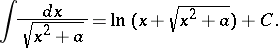 |
The dependence between variable quantities expressed by the logarithmic function was first considered by J. Napier in 1614.
The logarithmic function on the complex plane is an infinitely-valued function, defined for all values of the argument 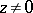 , and is denoted by
, and is denoted by  (or
(or 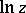 if no confusion arises). The single-valued branch of this function defined by
if no confusion arises). The single-valued branch of this function defined by
 |
where 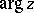 is the principal value of the argument of the complex number
is the principal value of the argument of the complex number  ,
, 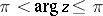 , is called the principal value of the logarithmic function. One has
, is called the principal value of the logarithmic function. One has
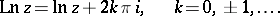 |
All values of the logarithmic function for negative real  are purely imaginary complex numbers. The first satisfactory theory of the logarithmic function for complex arguments was given by L. Euler in 1749; he started from the definition
are purely imaginary complex numbers. The first satisfactory theory of the logarithmic function for complex arguments was given by L. Euler in 1749; he started from the definition
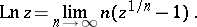 |
References
| [1] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Comments
The principal value of the logarithm maps the punctured complex  -plane
-plane  onto the strip
onto the strip  in the complex
in the complex  -plane. To fill the
-plane. To fill the 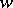 -plane one has to map infinitely many copies of the
-plane one has to map infinitely many copies of the  -plane, where for the
-plane, where for the  -th copy one has
-th copy one has 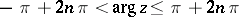 ,
,  . In this case
. In this case  is a branch point. The copies make up the so-called Riemann surface of the logarithmic function. Clearly,
is a branch point. The copies make up the so-called Riemann surface of the logarithmic function. Clearly,  is a one-to-one mapping of this surface
is a one-to-one mapping of this surface 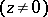 onto the
onto the 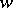 -plane. The derivative of the principal value is
-plane. The derivative of the principal value is  (as in the real case) for
(as in the real case) for 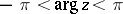 .
.
Instead of 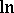 and
and 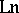 , many Western writers of post-calculus mathematics use
, many Western writers of post-calculus mathematics use 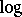 and
and  (see also (the editorial comments to) Logarithm of a number).
(see also (the editorial comments to) Logarithm of a number).
References
| [a1] | J.B. Conway, "Functions of one complex variable" , Springer (1973) |
| [a2] | E. Marsden, "Basic complex analysis" , Freeman (1973) |
| [a3] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
| [a4] | S. Saks, A. Zygmund, "Analytic functions" , PWN (1952) (Translated from Polish) |
| [a5] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
Logarithmic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_function&oldid=16249