Locally free sheaf
A sheaf of modules that is locally isomorphic to the direct sum of several copies of the structure sheaf. More precisely, let 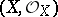 be a ringed space. A sheaf of modules
be a ringed space. A sheaf of modules 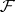 over
over 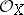 is said to be locally free if for every point
is said to be locally free if for every point 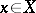 there is an open neighbourhood
there is an open neighbourhood 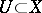 ,
, 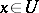 , such that the restriction
, such that the restriction 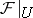 of
of 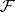 to
to 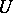 is a free sheaf of modules over
is a free sheaf of modules over 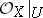 , that is, it is isomorphic to the direct sum of a set
, that is, it is isomorphic to the direct sum of a set 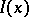 of copies of the structure sheaf
of copies of the structure sheaf 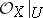 . If
. If 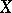 is connected and
is connected and 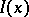 is finite, for example consisting of
is finite, for example consisting of  elements, then
elements, then  does not depend on the point
does not depend on the point  and is called the rank of the locally free sheaf
and is called the rank of the locally free sheaf 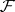 . Let
. Let 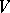 be a vector bundle of rank
be a vector bundle of rank  on
on 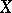 and let
and let 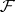 be the sheaf of germs of its sections. Then
be the sheaf of germs of its sections. Then 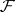 is a locally free sheaf of rank
is a locally free sheaf of rank  . Conversely, for every locally free sheaf
. Conversely, for every locally free sheaf 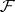 of rank
of rank  there is a vector bundle
there is a vector bundle 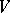 of rank
of rank  on
on 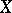 such that
such that 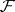 is the sheaf of germs of its sections (see [1], [2]); hence there is a natural one-to-one correspondence between the isomorphy classes of locally free sheaves of rank
is the sheaf of germs of its sections (see [1], [2]); hence there is a natural one-to-one correspondence between the isomorphy classes of locally free sheaves of rank  and the isomorphy classes of vector bundles of rank
and the isomorphy classes of vector bundles of rank  on
on 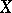 .
.
Example. Let 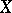 be a smooth connected algebraic variety of dimension
be a smooth connected algebraic variety of dimension  . Then the sheaf of regular differential forms
. Then the sheaf of regular differential forms 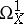 is a locally free sheaf of rank
is a locally free sheaf of rank  .
.
Let 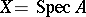 , a connected affine scheme, be the spectrum of the commutative ring
, a connected affine scheme, be the spectrum of the commutative ring  (cf. Spectrum of a ring), let
(cf. Spectrum of a ring), let 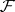 be a locally free sheaf of rank
be a locally free sheaf of rank  and let
and let 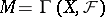 be the
be the  -module of its global sections. Then the
-module of its global sections. Then the 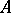 -module
-module 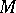 is projective and the mapping
is projective and the mapping 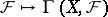 establishes a one-to-one correspondence between the set of classes (up to isomorphisms) of locally free sheaves of rank
establishes a one-to-one correspondence between the set of classes (up to isomorphisms) of locally free sheaves of rank  and the set of classes (up to isomorphisms) of projective
and the set of classes (up to isomorphisms) of projective 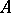 -modules of rank
-modules of rank  (see [2]).
(see [2]).
References
| [1] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Locally free sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_free_sheaf&oldid=15760