Locally flat imbedding
An imbedding (cf. Immersion)  of one topological manifold
of one topological manifold  into another
into another  such that for any point
such that for any point  there are charts in a neighbourhood
there are charts in a neighbourhood  of
of  and in a neighbourhood
and in a neighbourhood  of the point
of the point  in
in  in which the restriction of
in which the restriction of  to
to  linearly maps
linearly maps 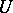 to
to 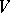 . In other words,
. In other words,  is locally linear in suitable coordinate systems. Equivalently: There are neighbourhoods
is locally linear in suitable coordinate systems. Equivalently: There are neighbourhoods 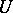 of a point
of a point  and
and  of the point
of the point 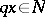 such that the pair
such that the pair  can be mapped homeomorphically onto a standard pair
can be mapped homeomorphically onto a standard pair  or
or 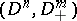 , where
, where 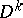 is the unit ball of the space
is the unit ball of the space 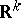 with centre at the origin and
with centre at the origin and  is the intersection of this ball with the half-space
is the intersection of this ball with the half-space  .
.
Any imbedding of a circle and an arc into a plane is locally flat; however, a circle or an arc can be imbedded in 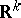 with
with 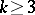 in a manner that is not locally flat (see Wild imbedding; Wild sphere). Any smooth imbedding is locally flat in the smooth sense (that is, in the definition the coordinates can be chosen to be smooth). A piecewise-linear imbedding need not be locally flat, not only in the piecewise-linear sense, but even not in the topological sense; for example, a cone with vertex in
in a manner that is not locally flat (see Wild imbedding; Wild sphere). Any smooth imbedding is locally flat in the smooth sense (that is, in the definition the coordinates can be chosen to be smooth). A piecewise-linear imbedding need not be locally flat, not only in the piecewise-linear sense, but even not in the topological sense; for example, a cone with vertex in 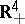 over a closed polygon knotted in the bounding plane
over a closed polygon knotted in the bounding plane 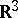 . For
. For 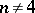 and
and 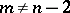 there is a homotopy criterion for an imbedding to be locally flat: For every point
there is a homotopy criterion for an imbedding to be locally flat: For every point  and neighbourhood
and neighbourhood  of the point
of the point  there is a neighbourhood
there is a neighbourhood 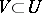 such that any loop in
such that any loop in 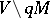 is homotopic to zero in
is homotopic to zero in 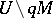 (local simple connectedness). If
(local simple connectedness). If 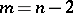 , then such a criterion holds for
, then such a criterion holds for 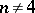 , but is essentially more complicated. For
, but is essentially more complicated. For  the question remains unsettled (1989). For
the question remains unsettled (1989). For 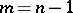 and
and 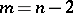 a locally flat imbedding has a topological normal bundle.
a locally flat imbedding has a topological normal bundle.
Comments
References
| [a1] | J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , Topology of manifolds , Markham (1970) |
Locally flat imbedding. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_flat_imbedding&oldid=15755