Locally compact skew-field
A set 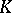 endowed with both the algebraic structure of a skew-field and a locally compact topology (cf. Locally compact space). It is required that the algebraic operations, that is, addition, multiplication and transitions to negative and inverse elements (the latter is defined only on the set of non-zero elements
endowed with both the algebraic structure of a skew-field and a locally compact topology (cf. Locally compact space). It is required that the algebraic operations, that is, addition, multiplication and transitions to negative and inverse elements (the latter is defined only on the set of non-zero elements 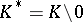 ) are continuous in the given topology. Since any skew-field is locally compact with respect to the discrete topology, it is assumed that the topology of
) are continuous in the given topology. Since any skew-field is locally compact with respect to the discrete topology, it is assumed that the topology of 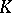 is not discrete.
is not discrete.
The study of locally compact skew-fields is based on the existence of a Haar measure on the locally compact group 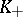 (the additive group of the skew-field). Let
(the additive group of the skew-field). Let 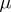 be a Haar measure on
be a Haar measure on 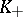 and let
and let 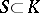 be a compact set in
be a compact set in 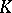 of positive measure. Then the formula
of positive measure. Then the formula
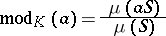 |
defines a homomorphism (the modulus) of the multiplicative group 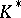 into the multiplicative group
into the multiplicative group 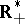 of positive real numbers. By definition one puts
of positive real numbers. By definition one puts 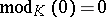 .
.
The "modulus" function satisfies the inequality
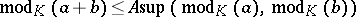 |
with some constant  . If this inequality holds for
. If this inequality holds for 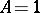 , then
, then 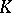 is said to be non-Archimedean, or ultrametric. Otherwise
is said to be non-Archimedean, or ultrametric. Otherwise 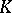 is called an Archimedean skew-field. A skew-field
is called an Archimedean skew-field. A skew-field 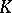 is Archimedean if and only if it is connected. Any Archimedean skew-field is isomorphic to either the field of real numbers, the field of complex numbers or the skew-field of quaternions.
is Archimedean if and only if it is connected. Any Archimedean skew-field is isomorphic to either the field of real numbers, the field of complex numbers or the skew-field of quaternions.
An ultrametric skew-field 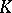 is totally disconnected (cf. Totally-disconnected space). The "modulus" function determines a non-Archimedean metric on
is totally disconnected (cf. Totally-disconnected space). The "modulus" function determines a non-Archimedean metric on 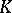 . Any such skew-field is an extension of finite degree of either the field
. Any such skew-field is an extension of finite degree of either the field 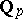 of rational
of rational 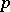 -adic numbers for some prime number
-adic numbers for some prime number 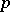 (in the case when
(in the case when 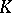 has characteristic 0) or the field
has characteristic 0) or the field 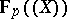 of formal power series over the field
of formal power series over the field  of
of 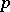 elements (in the case when
elements (in the case when 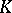 has characteristic
has characteristic 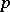 ). The field
). The field 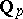 (respectively, the field
(respectively, the field 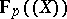 ) lies in the centre of
) lies in the centre of  . In each of these cases
. In each of these cases  is called a
is called a 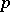 -skew-field, or a
-skew-field, or a 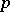 -field.
-field.
An ultrametric skew-field 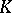 contains a unique maximal subring
contains a unique maximal subring 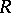 , defined by the condition
, defined by the condition
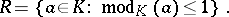 |
This ring is local (cf. Local ring). Its maximal ideal 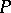 is defined by the condition
is defined by the condition
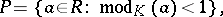 |
and all elements with modulus 1 are invertible in 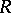 .
. 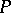 is a principal ideal, and the residue field
is a principal ideal, and the residue field 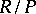 is a finite field of characteristic
is a finite field of characteristic  .
.
In the case when the 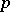 -skew-field is not commutative, it has dimension
-skew-field is not commutative, it has dimension 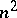 over its centre
over its centre 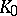 and ramification index
and ramification index  over
over 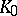 . Also, there is an intermediate field
. Also, there is an intermediate field 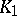 such that
such that 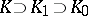 , where
, where 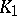 is an unramified extension of
is an unramified extension of 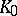 of degree
of degree  , and all automorphisms of
, and all automorphisms of 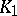 over
over 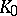 are induced by inner automorphisms of
are induced by inner automorphisms of 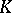 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | A. Weil, "Basic number theory" , Springer (1974) |
| [3] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [4] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [5] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
Locally compact skew-field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_compact_skew-field&oldid=14359