Locally algebraic operator

A linear operator such that for each element of the space under consideration there exists a polynomial in this operator (with scalar coefficients) annihilating this element.

Let 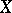be a linear space over a field 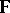. Let be the set of all linear operators with domains and ranges in 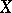and let

Denote by 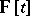the algebra of all polynomials in the variable 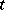and with coefficients in 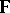. Usually, in applications it is assumed that the field 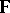is of characteristic zero and algebraically closed (cf. also Algebraically closed field; Characteristic of a field).

Thus, a linear operator 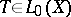is said to be locally algebraic if for any 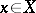there exists a non-zero polynomial such that 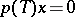(cf. [a1]). If there exists a non-zero polynomial such that 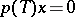for every 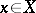, then 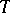is said to be algebraic (cf. Algebraic operator). Thus, an algebraic operator is locally algebraic, but not conversely.

A continuous locally algebraic operator acting in a complete linear metric space 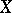is algebraic (cf. [a4]; for Banach spaces, see [a1]).

A locally algebraic operator 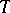acting in a complete linear metric space 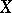(over the field 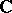of complex numbers) and that is right invertible (cf. Algebraic analysis) but not invertible, i.e.

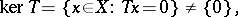is not continuous (cf. [a3]). The assumption about the completeness of is essential.

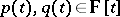If satisfies, for any , the conditions:

i) ;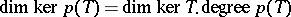

ii) ;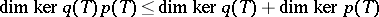

iii) 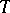is locally algebraic; then there exists an operator 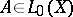such that

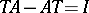(cf. [a2], [a5]). This means that 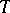is not an algebraic operator.

References

[a1]	I. Kaplansky, "Infinite Abelian groups" , Univ. Michigan Press (1954)
[a2]	J. Mikusiński, "Extension de l'espace linéaire avec dérivation" Studia Math. , 16 (1958) pp. 156–172
[a3]	D. Przeworska-Rolewicz, "Algebraic analysis" , PWN&Reidel (1988)
[a4]	D. Przeworska–Rolewicz, S. Rolewicz, "Equations in linear spaces" , PWN (1968)
[a5]	R. Sikorski, "On Mikusiński's algebraic theory of differential equations" Studia Math. , 16 (1958) pp. 230–236