Local structure of trajectories
of a quadratic differential
A description of the behaviour of the trajectories of a quadratic differential on an oriented Riemann surface in a neighbourhood of any point of this surface. Let  be an oriented Riemann surface and let
be an oriented Riemann surface and let 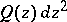 be a quadratic differential on
be a quadratic differential on 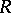 ; let
; let 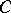 be the set of all zeros and simple poles of
be the set of all zeros and simple poles of 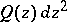 and let
and let 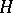 be the set of all poles of
be the set of all poles of 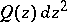 of order
of order 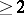 . The trajectories of
. The trajectories of 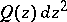 form a regular family of curves on
form a regular family of curves on 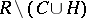 . Under an extension of the concept of a regular family of curves this remains true on
. Under an extension of the concept of a regular family of curves this remains true on 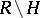 also. The behaviour of the trajectories in neighbourhoods of points of
also. The behaviour of the trajectories in neighbourhoods of points of 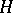 is significantly more complicated. A complete description of the local structure of trajectories is given below.
is significantly more complicated. A complete description of the local structure of trajectories is given below.
a) For any point 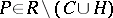 there is a neighbourhood
there is a neighbourhood 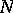 of
of 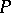 on
on 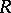 and a homeomorphic mapping of
and a homeomorphic mapping of 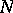 onto the disc
onto the disc 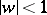 (
(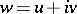 ) such that a maximal open arc of each trajectory in
) such that a maximal open arc of each trajectory in  goes to a segment on which
goes to a segment on which  is constant. Consequently, through each point of
is constant. Consequently, through each point of  there passes a trajectory of
there passes a trajectory of  that is either an open arc or a Jordan curve on
that is either an open arc or a Jordan curve on 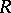 .
.
b) For any point 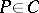 of order
of order 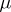 (
(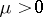 if
if 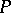 is a zero and
is a zero and 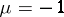 if
if 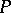 is a simple pole) there is a neighbourhood
is a simple pole) there is a neighbourhood 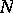 of
of 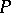 on
on 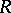 and a homeomorphic mapping of
and a homeomorphic mapping of 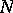 onto the disc
onto the disc 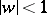 such that a maximal arc of each trajectory in
such that a maximal arc of each trajectory in  goes to an open arc on which
goes to an open arc on which 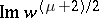 is constant. There are
is constant. There are 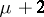 trajectories with ends at
trajectories with ends at 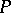 and with limiting tangential directions that make equal angles
and with limiting tangential directions that make equal angles 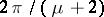 with each other.
with each other.
c) Let 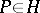 be a pole of order
be a pole of order 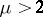 . If a certain trajectory has an end at
. If a certain trajectory has an end at 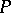 , then it tends to
, then it tends to 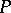 along one of
along one of 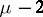 directions making equal angles
directions making equal angles 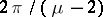 . There is a neighbourhood
. There is a neighbourhood 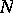 of
of 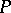 on
on 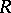 with the following properties: 1) every trajectory that passes through some point of
with the following properties: 1) every trajectory that passes through some point of 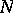 in each of the directions either tends to
in each of the directions either tends to 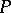 or leaves
or leaves  ; 2) there is a neighbourhood
; 2) there is a neighbourhood 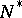 of
of 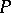 contained in
contained in 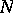 and such that every trajectory that passes through some point of
and such that every trajectory that passes through some point of 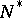 tends to
tends to 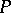 in at least one direction, remaining in
in at least one direction, remaining in 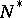 ; 3) if some trajectory lies entirely in
; 3) if some trajectory lies entirely in  and therefore tends to
and therefore tends to 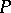 in both directions, then the tangent to this trajectory as
in both directions, then the tangent to this trajectory as 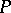 is approached in the corresponding direction tends to one of two adjacent limiting positions. The Jordan curve obtained by adjoining
is approached in the corresponding direction tends to one of two adjacent limiting positions. The Jordan curve obtained by adjoining 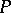 to this trajectory bounds a domain
to this trajectory bounds a domain 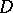 containing points of the angle formed by the two adjacent limiting tangents. The tangent to any trajectory that has points in common with
containing points of the angle formed by the two adjacent limiting tangents. The tangent to any trajectory that has points in common with 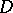 tends to these adjacent limiting positions as
tends to these adjacent limiting positions as 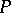 is approached in the two directions. By means of a suitable branch of the function
is approached in the two directions. By means of a suitable branch of the function 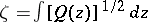 the domain
the domain 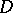 is mapped onto the half-plane
is mapped onto the half-plane 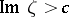 (where
(where  is a real number); and 4) for every pair of adjacent limiting positions there is a trajectory having the properties described in 3).
is a real number); and 4) for every pair of adjacent limiting positions there is a trajectory having the properties described in 3).
d) Let 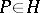 be a pole of order two and let
be a pole of order two and let  be the local parameter in terms of which
be the local parameter in terms of which 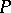 is the point
is the point 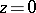 . Suppose that
. Suppose that 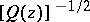 has (for some choice of the branch of the root) the following expansion in a neighbourhood of
has (for some choice of the branch of the root) the following expansion in a neighbourhood of 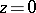 :
:
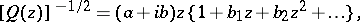 |
where  and
and 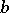 are real constants and
are real constants and 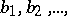 are complex constants. The structure of the images of the trajectories of the differential
are complex constants. The structure of the images of the trajectories of the differential 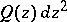 in the
in the  -plane is determined by which of the following three cases holds.
-plane is determined by which of the following three cases holds.
Case I: 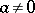 ,
, 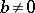 . For sufficiently small
. For sufficiently small 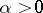 the image of each trajectory that intersects the disc
the image of each trajectory that intersects the disc 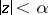 tends to
tends to 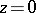 in one direction, and leaves
in one direction, and leaves 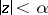 in the other direction. Both the modulus and the argument of
in the other direction. Both the modulus and the argument of  vary monotonically on the image of the trajectory in
vary monotonically on the image of the trajectory in 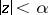 . Each image of a trajectory twists around the point
. Each image of a trajectory twists around the point 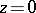 and behaves asymptotically like a logarithmic spiral.
and behaves asymptotically like a logarithmic spiral.
Case II: 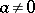 ,
, 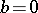 . For sufficiently small
. For sufficiently small 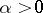 the image of every trajectory that intersects the disc
the image of every trajectory that intersects the disc 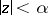 tends to
tends to 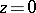 in one direction and leaves
in one direction and leaves 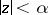 in the other direction. The modulus of
in the other direction. The modulus of  varies monotonically on the image of the trajectory in
varies monotonically on the image of the trajectory in  . Different images of trajectories have different limiting directions at the point
. Different images of trajectories have different limiting directions at the point 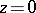 .
.
Case III: 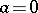 ,
, 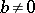 . For each
. For each 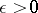 there is a number
there is a number 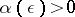 such that for
such that for 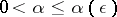 the image of a trajectory that intersects the circle
the image of a trajectory that intersects the circle  is a Jordan curve lying in the circular annulus
is a Jordan curve lying in the circular annulus 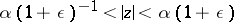 .
.
References
| [1] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
Comments
Cf. Quadratic differential for the notion of the trajectory of a quadratic differential.
This description is taken essentially from section 3.2 of [1]. For a detailed treatment of quadratic differentials see also [a1].
For the global structure see Global structure of trajectories.
References
| [a1] | K. Strebel, "Quadratic differentials" , Springer (1984) (Translated from German) |
| [a2] | F.P. Gardiner, "Teichmüller theory and quadratic differentials" , Wiley (1987) |
Local structure of trajectories. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_structure_of_trajectories&oldid=11783