Local limit theorems
in probability theory
Limit theorems for densities, that is, theorems that establish the convergence of the densities of a sequence of distributions to the density of the limit distribution (if the given densities exist), or a classical version of local limit theorems, namely local theorems for lattice distributions, the simplest of which is the local Laplace theorem.
Let  be a sequence of independent random variables that have a common distribution function
be a sequence of independent random variables that have a common distribution function  with mean
with mean  and finite positive variance
and finite positive variance  . Let
. Let  be the distribution function of the normalized sum
be the distribution function of the normalized sum
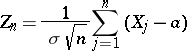 |
and let  be the normal
be the normal  -distribution function. The assumptions ensure that
-distribution function. The assumptions ensure that  as
as  for any
for any  . It can be shown that this relation does not imply the convergence of the density
. It can be shown that this relation does not imply the convergence of the density 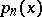 of the distribution of the random variable
of the distribution of the random variable 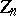 to the normal density
to the normal density
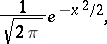 |
even if the distribution 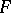 has a density. If
has a density. If 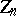 , for some
, for some  , has a bounded density
, has a bounded density 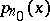 , then
, then
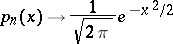 | (*) |
uniformly with respect to  . The condition that
. The condition that 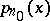 is bounded for some
is bounded for some 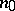 is necessary for (*) to hold uniformly with respect to
is necessary for (*) to hold uniformly with respect to  .
.
Let 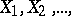 be a sequence of independent random variables that have the same non-degenerate distribution, and suppose that
be a sequence of independent random variables that have the same non-degenerate distribution, and suppose that 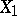 takes values of the form
takes values of the form 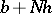 ,
, 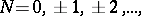 with probability 1, where
with probability 1, where 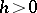 and
and 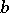 are constants (that is,
are constants (that is, 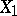 has a lattice distribution with step
has a lattice distribution with step 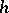 ).
).
Suppose that 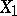 has finite variance
has finite variance 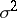 , let
, let 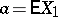 and let
and let
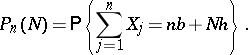 |
In order that
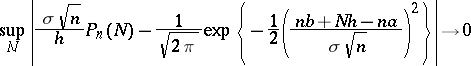 |
as 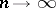 it is necessary and sufficient that the step
it is necessary and sufficient that the step  should be maximal. This theorem of B.V. Gnedenko is a generalization of the local Laplace theorem.
should be maximal. This theorem of B.V. Gnedenko is a generalization of the local Laplace theorem.
Local limit theorems for sums of independent non-identically distributed random variables serve as a basic mathematical tool in classical statistical mechanics and quantum statistics (see [7], [8]).
Local limit theorems have been intensively studied for sums of independent random variables and vectors, together with estimates of the rate of convergence in these theorems. The case of a limiting normal distribution has been most fully investigated (see [3], Chapt. 7); a number of papers have been devoted to local limit theorems for the case of an arbitrary stable distribution (see [2]). Similar investigations have been carried out for sums of dependent random variables, in particular for sums of random variables that form a Markov chain (see [5], ).
References
| [1] | B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) |
| [2] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) |
| [3] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
| [4] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [5] | S.Kh. Sirazhdinov, "Limit theorems for homogeneous Markov chains" , Tashkent (1955) (In Russian) |
| [6a] | V.A. Statulyavichus, "Limit theorems and asymptotic expansions for non-stationary Markov chains" Litovsk. Mat. Sb. , 1 (1961) pp. 231–314 (In Russian) (English abstract) |
| [6b] | V.A. Statulyavichus, "Limit theorems for sums of random variables that are connected in a Markov chain I" Litovsk. Mat. Sb. , 9 (1969) pp. 345–362 (In Russian) (English abstract) |
| [7] | A.Ya. Khinchin, "Mathematical foundations of statistical mechanics" , Dover, reprint (1949) (Translated from Russian) |
| [8] | A.Ya. Khinchin, "Mathematical foundations of quantum statistics" , Moscow-Leningrad (1951) (In Russian) |
Comments
References
| [a1] | R.N. Bhattacharya, R. Ranga Rao, "Normal approximations and asymptotic expansions" , Wiley (1976) |
| [a2] | V. Paulauskas, "Approximation theory in the central limit theorem. Exact results in Banach spaces" , Kluwer (1989) (Translated from Russian) |
Local limit theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_limit_theorems&oldid=11793