Local homology
The homology groups (cf. Homology group)
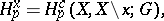 |
defined at points 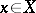 , where
, where 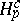 is homology with compact support. These groups coincide with the direct limits
is homology with compact support. These groups coincide with the direct limits
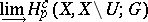 |
over open neighbourhoods 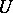 of
of  , and for homologically locally connected
, and for homologically locally connected 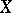 they also coincide with the inverse limits
they also coincide with the inverse limits
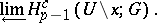 |
The homological dimension of a finite-dimensional metrizable locally compact space 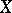 over
over 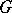 (cf. Homological dimension of a space) coincides with the largest value of
(cf. Homological dimension of a space) coincides with the largest value of  for which
for which 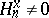 , and the set of such points
, and the set of such points 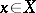 has dimension
has dimension  .
.
Let 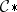 be the differential sheaf over
be the differential sheaf over 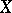 defined by associating with each open set
defined by associating with each open set 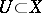 the chain complex
the chain complex 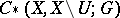 . The groups
. The groups 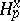 are the fibres of the derived sheaves
are the fibres of the derived sheaves 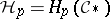 . For generalized manifolds,
. For generalized manifolds, 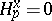 for
for 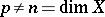 . In this case the homology sequence of the pair
. In this case the homology sequence of the pair 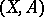 with coefficients in
with coefficients in 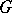 coincides with the cohomology of the pair
coincides with the cohomology of the pair 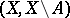 with coefficients in the sheaf
with coefficients in the sheaf 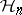 (Poincaré–Lefschetz duality). The similar facts for the local cohomology of locally compact spaces do not hold.
(Poincaré–Lefschetz duality). The similar facts for the local cohomology of locally compact spaces do not hold.
References
| [1] | E.G. Sklyarenko, "On the theory of generalized manifolds" Math. USSR Izv. , 5 : 4 (1971) pp. 845–858 Izv. Akad. Nauk SSSR Ser. Mat. , 35 (1971) pp. 831–843 |
| [2] | A.E. [A.E. Kharlap] Harlap, "Local homology and cohomology, homology dimension and generalized manifolds" Math. USSR Sb. , 25 : 3 (1975) pp. 323–349 Mat. Sb. , 96 (1975) pp. 347–373 |
Comments
References
| [a1] | A. Dold, "Lectures on algebraic topology" , Springer (1972) pp. Sect. IV.3 |
Local homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_homology&oldid=18081