Local field
A field that is complete with respect to a discrete valuation and has finite residue field. The structure of a local field 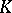 is well known: 1) if the characteristic of
is well known: 1) if the characteristic of 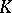 is
is  , then
, then 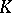 is a finite extension of the field
is a finite extension of the field 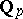 of
of 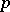 -adic numbers (cf.
-adic numbers (cf. 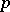 -adic number); 2) if the characteristic of
-adic number); 2) if the characteristic of 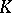 is greater than
is greater than  , then
, then 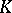 is isomorphic to the field
is isomorphic to the field 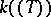 of formal power series over a finite field
of formal power series over a finite field 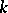 . Such fields are called local, in contrast to global fields (finite extensions of the fields
. Such fields are called local, in contrast to global fields (finite extensions of the fields 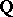 or
or 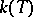 ), and are means for studying the latter. For cohomological properties of Galois extensions of local fields see [1], and also Adèle; Idèle; and Class field theory.
), and are means for studying the latter. For cohomological properties of Galois extensions of local fields see [1], and also Adèle; Idèle; and Class field theory.
To construct a class field theory of multi-dimensional schemes one uses a generalization of the concept of a local field. Namely, an  -dimensional local field is a sequence
-dimensional local field is a sequence 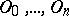 of complete discrete valuation rings together with isomorphisms
of complete discrete valuation rings together with isomorphisms
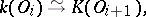 |
where 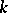 is the residue field and
is the residue field and 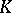 is the field of fractions of a ring
is the field of fractions of a ring 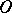 . Moreover,
. Moreover, 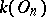 must be finite. There exists a structure theory for
must be finite. There exists a structure theory for  -dimensional local fields (see [3]).
-dimensional local fields (see [3]).
References
| [1] | J.-P. Serre, "Local fields" , Springer (1979) (Translated from French) |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [3] | A.N. Parshin, "Abelian coverings of arithmetic schemes" Soviet Math. Dokl. , 19 : 6 (1978) pp. 1438–1442 Dokl. Akad. Nauk SSSR , 243 (1978) pp. 855–858 |
Comments
The concept of a local field is sometimes extended to include that of discretely valued fields with arbitrary residue fields. There is a class field theory for local fields with perfect residue fields in terms of a certain fundamental group [a1], [a2]. For an account of the class field theory of  -dimensional local fields (in terms of algebraic
-dimensional local fields (in terms of algebraic 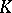 -theory) see also [a3]–[a5].
-theory) see also [a3]–[a5].
References
| [a1] | J.-P. Serre, "Sur les corps locaux à corps résiduel algébriquement clos" Bull. Soc. Math. France , 89 (1961) pp. 105–154 |
| [a2] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1971) pp. 648–674 ((Appendix: M. Hazewinkel, Classes de corps local)) |
| [a3] | K. Kato, "Class field theory and algebraic 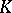 -theory" M. Raynaud (ed.) T. Shioda (ed.) , Algebraic geometry , Lect. notes in math. , 1016 , Springer (1983) pp. 109–126 -theory" M. Raynaud (ed.) T. Shioda (ed.) , Algebraic geometry , Lect. notes in math. , 1016 , Springer (1983) pp. 109–126 |
| [a4] | K. Kato, "Vanishing cycles, ramification of valuations and class field theory" Duke Math. J. , 55 (1987) pp. 629–661 |
| [a5] | A.N. [A.N. Parshin] Paršin, "Local class field theory" Proc. Steklov Inst. Math. , 165 (1985) pp. 157–185 Trudy Mat. Inst. Steklov. , 165 (1984) pp. 143–170 |
Local field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_field&oldid=11765