Liouville theorems
Liouville's theorem on bounded entire analytic functions: If an entire function  of the complex variable
of the complex variable 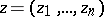 is bounded, that is,
is bounded, that is,
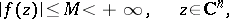 |
then 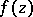 is a constant. This proposition, which is one of the fundamental results in the theory of analytic functions, was apparently first published in 1844 by A.L. Cauchy
is a constant. This proposition, which is one of the fundamental results in the theory of analytic functions, was apparently first published in 1844 by A.L. Cauchy
for the case 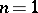 ; J. Liouville presented it in his lectures in 1847, and this is how the name arose.
; J. Liouville presented it in his lectures in 1847, and this is how the name arose.
Liouville's theorem can be generalized in various directions. For example, if 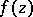 is an entire function in
is an entire function in 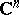 and
and
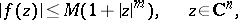 |
for some integer 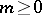 , then
, then 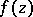 is a polynomial in the variables
is a polynomial in the variables 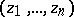 of degree not exceeding
of degree not exceeding 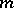 . Moreover, if
. Moreover, if  is a real-valued harmonic function in the number space
is a real-valued harmonic function in the number space 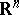 ,
,  , and
, and
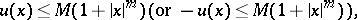 |
 , then
, then 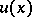 is a harmonic polynomial in
is a harmonic polynomial in 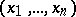 of degree not exceeding
of degree not exceeding 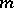 (see also ).
(see also ).
Liouville's theorem on conformal mapping: Every conformal mapping of a domain in a Euclidean space 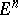 with
with 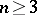 can be represented as a finite number of compositions of very simple mappings of four kinds — translation, similarity, orthogonal transformation, and inversion. It was proved by J. Liouville in 1850 (see [2], Appendix 6).
can be represented as a finite number of compositions of very simple mappings of four kinds — translation, similarity, orthogonal transformation, and inversion. It was proved by J. Liouville in 1850 (see [2], Appendix 6).
This Liouville theorem shows the poverty of the class of conformal mappings in space, and from this point of view it is very important in the theory of analytic functions of several complex variables and in the theory of quasi-conformal mapping.
References
| [1] | A.L. Cauchy, C.R. Acad. Sci. Paris , 19 (1844) pp. 1377–1384 |
| [2] | G. Monge, "Application de l'analyse à la géométrie" , Bachelier (1850) pp. 609–616 |
| [3] | A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian) |
| [4] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
E.D. Solomentsev
Liouville's theorem on approximation of algebraic numbers is a theorem stating that an algebraic irrationality cannot be very well approximated by rational numbers. Namely, if 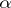 is an algebraic number of degree
is an algebraic number of degree 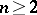 and
and 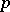 and
and  are any positive integral rational numbers, then
are any positive integral rational numbers, then
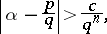 |
where  is a positive constant depending only on
is a positive constant depending only on 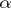 and expressible in explicit form in terms of quantities associated with
and expressible in explicit form in terms of quantities associated with 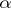 .
.
By means of this theorem J. Liouville [1] was the first to construct non-algebraic (transcendental) numbers (cf. Transcendental number). Such a number is, for example,
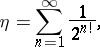 |
which is a series with rapidly-decreasing terms.
For 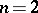 Liouville's theorem gives the best possible result. For
Liouville's theorem gives the best possible result. For 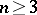 the theorem has often been strengthened. In 1909 A. Thue [2] established that for algebraic numbers
the theorem has often been strengthened. In 1909 A. Thue [2] established that for algebraic numbers 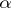 of degree
of degree 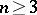 and for
and for 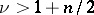 ,
,
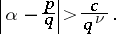 | (1) |
C.L. Siegel [3] improved Thue's result by showing that (1) is satisfied if
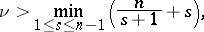 |
where  is an integer, in particular, for
is an integer, in particular, for  . Later F.J. Dyson [4] proved that (1) holds when
. Later F.J. Dyson [4] proved that (1) holds when 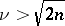 . Finally, K.F. Roth [5] established that (1) holds for any
. Finally, K.F. Roth [5] established that (1) holds for any 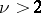 . Roth's result is the best of its kind, since any irrational number
. Roth's result is the best of its kind, since any irrational number  , algebraic or not, has infinitely many rational approximations
, algebraic or not, has infinitely many rational approximations 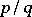 satisfying the inequality
satisfying the inequality
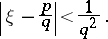 | (2) |
All strengthenings of Liouville's theorem mentioned above have one important deficiency — they are non-effective; namely: Their methods of proof do not make it possible to establish how the constant 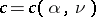 in inequality (1) depends on
in inequality (1) depends on  and
and  . Effective strengthenings of Liouville's theorem have been obtained (see [6]–[8]), but only for values of
. Effective strengthenings of Liouville's theorem have been obtained (see [6]–[8]), but only for values of  that differ little from
that differ little from  .
.
References
| [1] | J. Liouville, "Sur les classes très étendues de quantités dont la valeur n'est ni algébrique, ni même réductible à des irrationelles algébriques" C.R. Acad. Sci. Paris , 18 (1844) pp. 883–885; 910–911 |
| [2] | A. Thue, "Ueber Annäherungswerte algebraischer Zahlen" J. Reine Angew. Math. , 135 (1909) pp. 284–305 |
| [3] | C.L. Siegel, "Approximation algebraischer Zahlen" Math. Z. , 10 (1921) pp. 173–213 |
| [4] | F.J. Dyson, "The approximation to algebraic numbers by rationals" Acta Math. , 79 (1947) pp. 225–240 |
| [5] | K.F. Roth, "Rational approximation to algebraic numbers" Mathematika , 2 (1955) pp. 1–20; 168 |
| [6] | A. Baker, "Contributions to the theory of Diophantine equations I" Philos. Trans. Roy. Soc. London Ser. A , 263 (1968) pp. 173–191 |
| [7] | V.G. Sprindzhuk, "Rational approximations to algebraic numbers" Math. USSR Izv. , 5 (1971) pp. 1003–1019 Izv. Akad. Nauk SSSR Ser. Mat. , 35 (1971) pp. 991–1007 |
| [8] | N.I. Fel'dman, "An effective refinement of the exponent in Liouville's theorem" Math. USSR Izv. , 5 : 5 (1971) pp. 985–1002 Izv. Akad. Nauk. SSSR Ser. Mat. , 35 : 5 (1971) pp. 973–990 |
S.A. Stepanov
Comments
Rational approximations 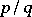 for which (2) holds can be found among the convergents of the continued fraction expansion of
for which (2) holds can be found among the convergents of the continued fraction expansion of 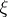 .
.
Liouville's theorem on the conservation of phase volume: The volume 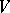 of any domain
of any domain 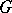 of the
of the 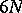 -dimensional phase space
-dimensional phase space 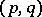 (the space of components of the momenta
(the space of components of the momenta 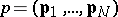 and coordinates
and coordinates 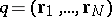 of each of the
of each of the 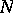 particles of a classical system with potential forces of interaction) does not change in the course of time,
particles of a classical system with potential forces of interaction) does not change in the course of time,
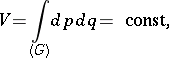 |
if all points of this domain are shifted in accordance with the equations of classical mechanics. The assertion is a consequence of the fact that the Jacobian of the transformation from the variables 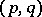 (at time
(at time 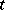 ) to the variables
) to the variables 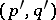 (at time
(at time 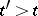 ) in accordance with the equations of motion (for example, in the form of Hamilton's equations) is equal to one. The quantity
) in accordance with the equations of motion (for example, in the form of Hamilton's equations) is equal to one. The quantity 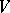 is one of the integral invariants of Poincaré, and the theorem is a consequence of their existence. Liouville's theorem is used in statistical mechanics of classical systems (see Liouville equation). It was proposed by J. Liouville in 1851.
is one of the integral invariants of Poincaré, and the theorem is a consequence of their existence. Liouville's theorem is used in statistical mechanics of classical systems (see Liouville equation). It was proposed by J. Liouville in 1851.
I.A. Kvasnikov
Liouville theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville_theorems&oldid=19033