Liouville-Łojasiewicz inequality
A Liouville inequality is one embodying the principle in number theory that algebraic numbers cannot be very well approximated by rational numbers or, equivalently, that integral polynomials cannot be small and non-zero at algebraic numbers (cf. also Liouville theorems). A Łojasiewicz inequality gives a lower bound for functions in terms of the distance to common zeros.
These features can be combined [a5] in the following Liouville–Łojasiewicz inequality. Let each  have total degree at most
have total degree at most  and coefficients of absolute value at most
and coefficients of absolute value at most  . For
. For  , let
, let  be greater than or equal to the largest absolute value of the coordinates of
be greater than or equal to the largest absolute value of the coordinates of  and let
and let  be less than or equal to the distance from
be less than or equal to the distance from  to the common zeros
to the common zeros  of
of 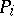 . Then there are explicit constants
. Then there are explicit constants 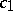 ,
, 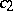 ,
, 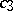 depending on
depending on  such that
such that
 |
where 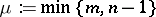 ,
, 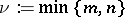 .
.
Over arbitrary fields with an absolute value, the lower bound takes the form 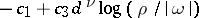 , cf. [a4], [a2] and [a1] (in the last citation, the polynomials
, cf. [a4], [a2] and [a1] (in the last citation, the polynomials 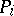 are replaced by ideals
are replaced by ideals  and
and 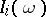 are taken to be the values of fixed Chow coordinates of
are taken to be the values of fixed Chow coordinates of 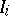 ). In this setting, M. Hickel [a3] obtains the optimal involvement of
). In this setting, M. Hickel [a3] obtains the optimal involvement of 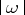 at the right-hand side. Actually, the above arithmetic inequality holds with
at the right-hand side. Actually, the above arithmetic inequality holds with  .
.
If, when working over 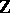 ,
, 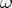 denotes a zero of an unmixed ideal
denotes a zero of an unmixed ideal 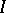 and
and 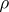 denotes the distance from
denotes the distance from 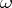 to the zeros of
to the zeros of 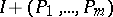 , then the above upper bound holds with
, then the above upper bound holds with  ,
, 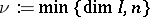 , with
, with 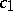 replaced by
replaced by  , and
, and 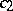 by
by 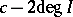 . When
. When 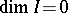 , the zeros
, the zeros 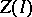 of
of 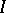 have algebraic coordinates. When
have algebraic coordinates. When 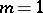 and
and 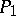 does not vanish at any point of
does not vanish at any point of  , then one obtains an explicit lower bound on
, then one obtains an explicit lower bound on 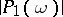 , i.e. a Liouville inequality.
, i.e. a Liouville inequality.
References
| [a1] | J. Kollár, "Effective Nullstellensatz for arbitrary ideals" J. Europ. Math. Soc. (JEMS) , 1 (1999) pp. 313–337 |
| [a2] | S. Ji, J. Kollár, B. Shiffman, "A global Łojasiewicz inequality for algebraic varieties" Trans. Amer. Math. Soc. , 329 (1992) pp. 813–818 |
| [a3] | M. Hickel, "Solution d'une conjecture de C. Berenstein–A. Yger et invariants de contact à l'infini" Prepubl. Lab. Math. Pures Univ. Bordeaux I , 118 : jan. (2000) |
| [a4] | W.D. Brownawell, "Bounds for the degrees in the Nullstellensatz" Ann. of Math. , 126 (1987) pp. 577–591 |
| [a5] | W.D. Brownawell, "Local diophantine Nullstellen equalities" J. Amer. Math. Soc. , 1 (1988) pp. 311–322 |
Liouville-Łojasiewicz inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville-%C5%81ojasiewicz_inequality&oldid=11458