Linking coefficient

An integer or fraction associated with two disjoint cycles and in an -dimensional manifold whose homology classes are members of the torsion subgroups of the integral homologies and , respectively. The simplest example is the linking coefficient of two non-intersecting closed rectifiable curves in , given by the so-called Gauss integral:

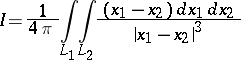(here and are the radius vectors of 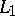and ).

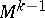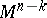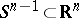The concept of the linking coefficient generalizes to the case of closed oriented manifolds and in : the linking coefficient is equal to the degree of the mapping (cf. Degree of a mapping) of the oriented direct product into the sphere , where , , is the point at which is cut by a ray through the origin parallel to the vector . The linking coefficient is equal to the intersection index (in homology) of any -chain such that with the cycle , divided by 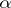. This number is independent of the choice of . If the roles of the cycles and 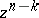are interchanged, the linking coefficient is multiplied (in the orientable case) by . If either of the cycles is replaced by a homological cycle in the complement to the other cycle, the linking coefficient remains the same. This is the basis for the linking interpretation of Alexander duality. If one of the cycles is replaced by a homological cycle, the linking coefficient varies by an integer, thus defining a pairing of torsion subgroups in and with values in the quotient group , where 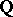denotes the set of rational numbers. This pairing establishes a Pontryagin duality between them. In particular, considering the torsion subgroup of in the case 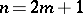, it defines a non-degenerate quadratic form of self-linkings with values in 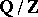, which is a homotopy invariant of the manifold. For example, this was what led to the first observations of asymmetric manifolds, which were particular lens manifolds (cf. Lens space).

Linking coefficients are also considered in other coefficient domains; for example, if a group is acting freely on the manifold, the homology groups are group modules and the linking coefficient is defined in a suitably localized group ring.

References

[1]	H. Seifert, W. Threlfall, "Lehrbuch der Topologie" , Chelsea, reprint (1980)
[2]	L.S. Pontryagin, "Smooth manifolds and their applications in homotopy theory" Transl. Amer. Math. Soc. , 11 (1959) pp. 1–114 Trudy Mat. Inst. Steklov. , 45 (1955)

References

[a1]	E.H. Spanier, "Algebraic topology" , Springer (1978)