Linear system of differential equations with almost-periodic coefficients
A system of ordinary differential equations
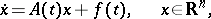 | (1) |
where  ,
, 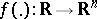 are almost-periodic mappings (cf. Almost-periodic function). In coordinate form one has
are almost-periodic mappings (cf. Almost-periodic function). In coordinate form one has
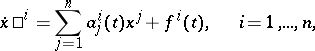 |
where 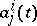 and
and 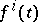 ,
, 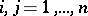 , are almost-periodic real-valued functions. Such systems arise in connection with Bohr almost-periodic functions (see [1]). Interest in a narrower class of systems (where
, are almost-periodic real-valued functions. Such systems arise in connection with Bohr almost-periodic functions (see [1]). Interest in a narrower class of systems (where 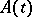 and
and 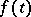 are quasi-periodic mappings, cf. Quasi-periodic function) arose much earlier in connection with the examination of variational equations along conditionally-periodic solutions of the equations of celestial mechanics.
are quasi-periodic mappings, cf. Quasi-periodic function) arose much earlier in connection with the examination of variational equations along conditionally-periodic solutions of the equations of celestial mechanics.
If the homogeneous system
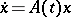 | (2) |
is a system with integral separation (see Integral separation condition), then it reduces to a diagonal system 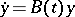 with almost-periodic coefficients by an almost-periodic (with respect to
with almost-periodic coefficients by an almost-periodic (with respect to 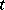 ) Lyapunov transformation
) Lyapunov transformation 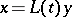 ; that is, it reduces to a system for which there is a basis of
; that is, it reduces to a system for which there is a basis of 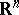 , independent of
, independent of  , consisting of vectors that are eigen vectors of the operator
, consisting of vectors that are eigen vectors of the operator 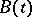 for every
for every 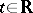 . In coordinates with respect to this basis the system
. In coordinates with respect to this basis the system 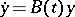 is written in diagonal form:
is written in diagonal form:
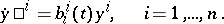 |
The set of systems with integral separation is open in the space of systems (2) with almost-periodic coefficients, endowed with the metric
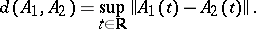 |
The following theorem holds. Let 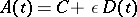 , where
, where 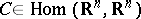 , let the eigen values of
, let the eigen values of  all be real and distinct, and let
all be real and distinct, and let 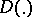 be an almost-periodic mapping
be an almost-periodic mapping 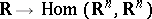 . Then there is an
. Then there is an 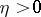 such that for all
such that for all  with
with 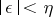 the system (2) reduces to a diagonal system with almost-periodic coefficients, by an almost-periodic (with respect to
the system (2) reduces to a diagonal system with almost-periodic coefficients, by an almost-periodic (with respect to  ) Lyapunov transformation.
) Lyapunov transformation.
For an almost-periodic mapping 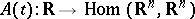 the following four assertions are equivalent: 1) for every almost-periodic mapping
the following four assertions are equivalent: 1) for every almost-periodic mapping 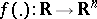 there is an almost-periodic solution of the system (1); 2) there is exponential dichotomy of solutions of the system (2); 3) none of the systems
there is an almost-periodic solution of the system (1); 2) there is exponential dichotomy of solutions of the system (2); 3) none of the systems 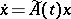 , where
, where 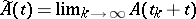 , has non-zero bounded solutions; and 4) for every bounded mapping
, has non-zero bounded solutions; and 4) for every bounded mapping 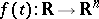 there is a bounded solution of the system (1).
there is a bounded solution of the system (1).
References
| [1] | H. Bohr, "Almost-periodic functions" , Chelsea, reprint (1947) (Translated from German) |
| [2] | J. Favard, "Leçons sur les fonctions presque-périodiques" , Gauthier-Villars (1933) |
| [3] | N.P. Erugin, "Linear systems of ordinary differential equations with periodic and quasi-periodic coefficients" , Acad. Press (1966) (Translated from Russian) |
| [4] | J.L. Massera, J.J. Shäffer, "Linear differential equations and function spaces" , Acad. Press (1986) |
| [5] | E. Mukhamadiev, "On invertibility of differential operators in the space of continuous functions bounded on the real axis" Soviet Math. Dokl. , 12 (1971) pp. 49–52 Dokl. Akad. Nauk SSSR , 196 : 1 (1971) pp. 47–49 |
| [6] | Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
Comments
See also Differential equation, ordinary.
References
| [a1] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
Linear system of differential equations with almost-periodic coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_system_of_differential_equations_with_almost-periodic_coefficients&oldid=17504