Linear summation method
A summation method (cf. Summation methods) having the properties of linearity:
1) if the series 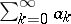 is summable by the summation method to the sum
is summable by the summation method to the sum 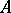 , then the series
, then the series 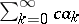 is summable by this method to the sum
is summable by this method to the sum 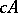 ;
;
2) if the series 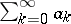 ,
,  are summable by the summation method to
are summable by the summation method to 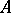 and
and 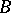 respectively, then the series
respectively, then the series 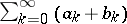 is summable by this method to the sum
is summable by this method to the sum 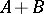 .
.
All most widespread summation methods are linear; in particular, a matrix summation method and a semi-continuous summation method. There are non-linear summation methods. For example, the method in which summability of a series to the sum 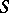 is defined by the existence of the limit
is defined by the existence of the limit 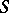 of the sequence
of the sequence 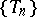 , where
, where
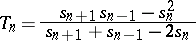 |
(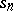 are the partial sums of the series), is not linear.
are the partial sums of the series), is not linear.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.F. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 (1976) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Linear summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_summation_method&oldid=17658