Linear representation, invariant of a
From Encyclopedia of Mathematics
A vector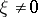 
in the space 
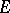of a representation 
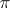of a group 
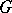(cf. Representation of a group) such that 
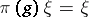for all 
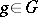. An invariant of a linear representation 
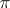of a Lie algebra 
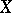is a vector 
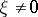in the space 
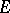of 
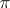such that 
for all 
. In particular, if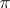 
is a representation of a linear group in a space of multilinear functions, the given definition of the invariant of a linear representation coincides with the classical definition. The invariants of a linear representation arising from restricting an irreducible representation to a subgroup play an important role in the representation theory of Lie groups and Lie algebras (cf. Representation of a Lie algebra).
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
Comments
References
| [a1] | T.A. Springer, "Invariant theory" , Lect. notes in math. , 585 , Springer (1977) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
| [a3] | Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) |
How to Cite This Entry:
Linear representation, invariant of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_representation,_invariant_of_a&oldid=12505
Linear representation, invariant of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_representation,_invariant_of_a&oldid=12505
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article