Linear representation
From Encyclopedia of Mathematics
A homomorphism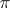 
of a group (respectively an algebra, ring, semi-group) 
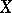into the group of all invertible linear operators on a vector space 
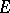(respectively, into the algebra, ring, multiplicative semi-group of all linear operators on 
). If 
is a topological vector space, then a linear representation of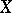 
on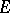 
is a representation whose image contains only continuous linear operators on 
. The space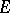 
is called the representation space of 
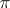and the operators 
, 
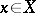, are called the operators of the representation 
.
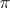References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
Comments
References
| [a1] | C.W. Curtis, I. Reiner, "Methods of representation theory" , 1–2 , Wiley (Interscience) (1981–1987) |
| [a2] | J.-P. Serre, "Répresentations linéaires des groupes finis" , Hermann (1967) |
| [a3] | A.I. Shtern, "Theory of group representations" , Springer (1982) (Translated from Russian) |
How to Cite This Entry:
Linear representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_representation&oldid=16731
Linear representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_representation&oldid=16731
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article