Linear classical group
From Encyclopedia of Mathematics
A group of non-singular linear transformations of a finite-dimensional vector space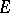 
over a skew-field 
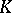that is a classical group (see also Linear group). The most important types of linear classical groups are the following: the general linear group 
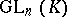, the special linear group 
and the unitary group 
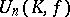(where 
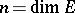and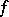 
is a Hermitian or skew-Hermitian form on 
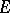, relative to an involution of 
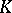). When 
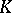is also commutative, special important cases are: the symplectic group 
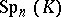and the orthogonal group 
(
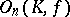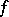a quadratic form on 
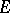and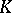 
of characteristic not 2).
How to Cite This Entry:
Linear classical group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_classical_group&oldid=11422
Linear classical group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_classical_group&oldid=11422
This article was adapted from an original article by V.L. Popov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article