Lindelöf space
finally-compact space
A topological space  such that every open covering (cf. Covering (of a set)) of it contains a countable subcovering. For example, a space with a countable base is a Lindelöf space; every quasi-compact space is a Lindelöf space. Every closed subspace of a Lindelöf space is a Lindelöf space. For every continuous mapping
such that every open covering (cf. Covering (of a set)) of it contains a countable subcovering. For example, a space with a countable base is a Lindelöf space; every quasi-compact space is a Lindelöf space. Every closed subspace of a Lindelöf space is a Lindelöf space. For every continuous mapping 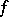 of a Lindelöf space
of a Lindelöf space  into a topological space, the subspace
into a topological space, the subspace  of the latter is a Lindelöf space. Every Hausdorff space that is the union of a countable family of compact (Hausdorff) sets is a Lindelöf space. Every regular Lindelöf space is paracompact (cf. Paracompact space). The product of a Lindelöf space and a compact (Hausdorff) space is a Lindelöf space.
of the latter is a Lindelöf space. Every Hausdorff space that is the union of a countable family of compact (Hausdorff) sets is a Lindelöf space. Every regular Lindelöf space is paracompact (cf. Paracompact space). The product of a Lindelöf space and a compact (Hausdorff) space is a Lindelöf space.
Lindelöf space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_space&oldid=23392